1take differential elements in d form of strips between n den integrate???
I dont know if this can be solved.. (I havent so far..) but this question just stuck me when i was seeing another one..
On a solid sphere of radius R, or resistivity σ, there are two points a, b on the equatorial line at a distance x from each other...
What is the equivalent resistance between the two points...?
-
UP 0 DOWN 0 0 14
14 Answers
1
62I guess you will have to do that.. but i can think of a method to do that without involving triple integrals. even those seem a bit complex to me!
24just a try..
isnt it simply a parallel connection of 2 resistances??
3just asked whether superposition principle help me newhere,sir i asked since a similar type of pbm we have done for finding the gravitional potential of sphere with a hole.Also the similarities.
11I don't think that helps either, rohit!
What at amx u can do is to take an elementary strip of width dx at a dist x from the centre ....
dR=σ2πx2πxdx=σdx...
Now?
1its very difficult to imagine what you all are discussing can anyone please post a simple diagram to illustrate your point
1wont it be an infinite parallel combination of strips taken ??..i think its so.coz its a solid sphere....sir,can i think like dis??
24I dont know how I am going ot explain my statement with a figure..but still....
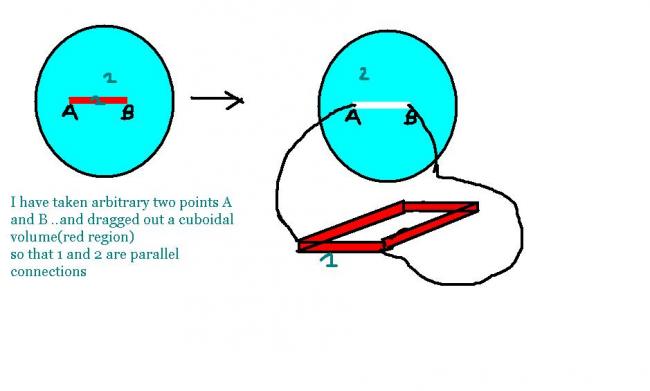
is it OK sir ???
24equitorial would mean any diametrical line.....like equator of earth..
66I don't think we can find the resistance across the two points in analytical form. Taking differential elements is okay. But the problem is how do one choose which kind of differential element one uses. The formula R = ÏlA requires that the current density vector be parallel to the length and perpendicular to the cross-section.
In this case the current density lines are going to be very much like the field lines of a dipole and I don't think there are nice ways to choose the differential elements.
However, I need to make sure. Still trying out some more things.