106sir where do we take the origin?
Part 1
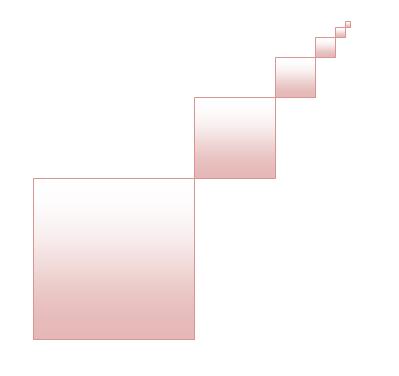
here the radius side of the successive square is half of the original one... (The whole thing goes to infinity)
Side of the Largest square is 1.
Part 2
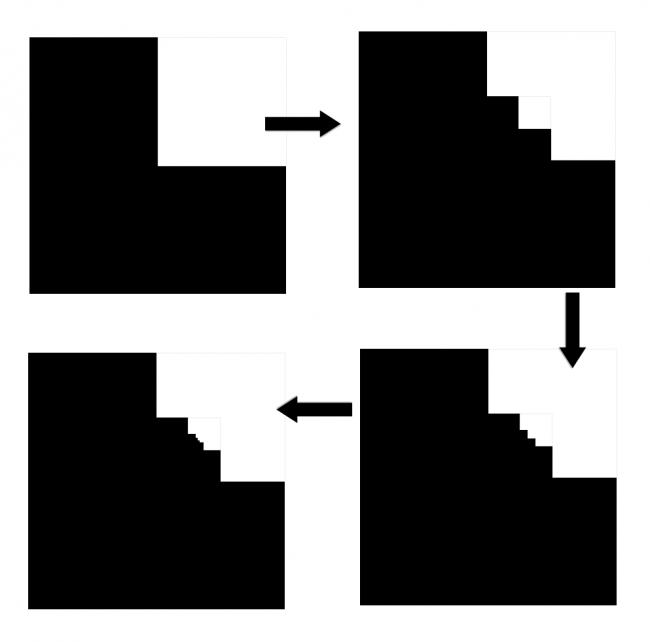
Find the CM of this system...
Here you successively add the same kind of cut squares.. Infinitely many times
First take a square of side one. Remove 1/4th of ti.. then add a square of 1/4th the side of original side and repeat the same thing...
Take the origin as the lower most left point of the bottom square...
-
UP 0 DOWN 0 2 16
16 Answers
62Take it whereever you want...
for instance the left bottom most point...
106sir:
here the radius of the successive square is half of the original one... ??
1R =\frac{ M + \frac{M}{3}(1+R)}{4M/3}
R gives us the x as well as y coordinate of COM
M is mass of the first block
I suppose there is a small error but this was the best method i could think of
1Yes I realized as much...
the answer to part I
(57,57)
to part II
(37,37)
____________________________________
for part I
I used
R =\frac{ M.(1/2) + \frac{M}{3}(1+R/2)}{4M/3}
symbols have the same meaning as in #9
similarly for part II
1Someone please confirm the answer
PS : I have assumed uniform density
62I have not verified the 2nd part... but the 1st one is correct...
can someone post the exact expressoin for the 2nd part?
1I just did not want to end this thread here so I left the expression for part II
however here it is
R\, =\, \frac{3M(\frac{5}{12})+\frac{M}{5}(\frac{R}{4}+\frac{1}{2})}{\frac{16M}{5}}
here 3M is the mass of the first block
taken side of largest block as 1
1one doubt sir.....is the mass of each square same or is the material same!!!!!
