Find the minimum velocity required to send the ball to the top of this infinite structure....
Keep in mind:
The successive radius are half of the original ones.....
there are infintely many such.
The lowest loop has radius R, the 2nd R/2 , 3rd R/4 and so on...
The mass is of zero size
Velocity at the top is not zero in a single loop case! (So be careful when you are conserving energy!)
24we also have to prove that normal reaction doent become zero when the ball si moving in a particualr semi circle...
I think thats what Nishant sir means
1Since no one has posted even one correctly directed argument :-
Let the speed required be u.
u^{2}= 4gR + u^{2}/2\, \Rightarrow u=\sqrt{8gR}
The reason virang got the right answer is that energy conservation is justified in this situation
because as the limiting value of R at the top is 0.. final velocity is also 0
24One point I cant understand is that why all this discussion on whether it will follow path or not(i.e slip away) is being discussed ??
If we provide the body sufficient velocity at bottom to reach the top of a particular ring with some non zero velcoity then there is no scope it would leave the path
Also we are working on concave surface and not convex surface...
for which we have to worry so much
If I ma wrong in whatever I said...plz thrash me[6]
3sir in my pic,if we write the force eqn at point B we will get -N-mg=mv2/rn which is not possible isnt it,or am i rong.
we can have a chance if N+mg=mv2/rn-1.
but this is not the case u mentioned already.
62you can put the question that way to... there is not much fo a problem...
1the only case possible is that the rings are hallow tubes and the mass is moving inside it otherwise i dont see the logic behind it
1i dont know but i have a very weird feeling that this cant be achieved
62virang the right answer is infact √8gr
I want the justification
Also.. do you add velocity that way!!
11See i think my first answer is wrong
Now,
The velocity at the top part of the single loop has to be √gR
therefore the energy required for a single loop
mg2R + mgR/2 = 5mgR/2
Therefore total energy =
5mgR/2 (1 + 1/2 + 1/4 + ....... + 1/∞)
= 5mgR
Therefore the velocity =
v = √(10gR)
1As an afterthought I deleted whatever analysis i had posted.
However, the answer that virang got the first time is correct (maybe for a reason he did not mention)
minimum velocity required is √8gR.
62Some Clarification:
The mass is very very small.. and the upper ring is placed so that the lower mass just enters the next ring when it comes out...
1when the mass reaches the end of first semicircle:can any1 exlplain that why would it not come out tangentialy!!!!!.....is the reason that the normal reaction is not zero that's why!!!!!!
3sir i know dat but i have a dbt in writing the force eqn.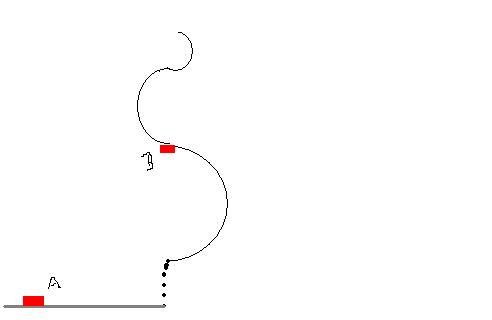
pls see the fig.i thot that limiting value of Normal force will act on the pt B.so the pt is an inflexion pt of the structure so what will be the direction of normal force,
62yes it does.. but you have to prove that quantitatively..
Just a non zero velocity does not help... I mean for a single cirlce it turns out to be √gr
1At the topmost point the velocity is not zero. This helps it to continue into the 2nd circle.....and again it reaches a cert. vel. at the top which helps it to move into the 3rd and so on.....right ?
62lol... no this is not what i am asking.. (for this question, the reason is very simple..)
take the case of the single circular loop, There we cannot conserve energy directly by saying that at the topmost point, the velocity is zero... because the mass would have detached from the surface of the circle...
Keeping this in mind, can you explain why this will never take off from the whole circular path...
* This is not difficult
1Just an idiotic guess work sir...pls don't kill me....
There are a few detached pts. in the path As soon as the body gets to the top a circle it drops to the bottom of the 2nd circle and so on........ :-(
62but how do you justify that the ball will never leave the surface.. like it does in a single looped circle?
1How on earth could i do this ..............!!!!!!!!!
I think the correct procedure....
12mv2 = mg.4R
I had idiotically taken the height 2R
So, i think v=√8gR does it.
And the ball will face a certain minimum velocity at each new circle that helps it to continue with its motion in the loop.....it doesn't get detached at any point....else it will go up a cert. distance in the loop and fall back in the same path....right ?
62Good doubt sankara...
@virang... same doubt.. you have not shown that the ball will stay touching the walls all the time...
Aveeek.. with your velocity, the balll wil not even reach the top of the first semicircle! :P
minimum needed is √5gr > √4gr (ie your value)
1At the top, min vel = √(gR/2n)
At lowermost pt. vel = v (min.)
12mv2 = 12mgR2n + mg.2.R
As n=∞
v2 = 4gR
hence v=2√gR
I hope it's right
3i have a dbt virang,whether with this velocity the body doesnt loses its contact with the structure thru out the motion.
112mgR is the potential at the top of the first half cirlce
Therefore the total potential required
= 2mgR +mgR +mgR/2 + mgR/4 + ........ till infinity
= 2mgR( 1 +1/2 + 1/4 + ...... ∞)
( 1 +1/2 + 1/4 + ...... ∞) is a G.P = 2
= 2mgR(2)
=4mgR
4mgR = mv2/25
v2 = 8gR
v = 2√2gR
