30
30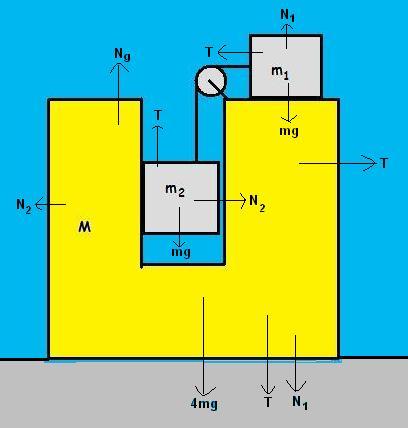
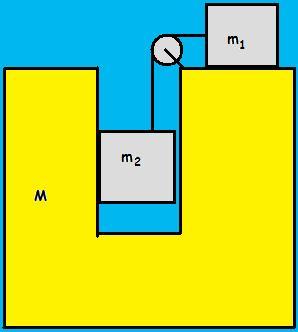
Now, first things first, let us assume the acceleration of the big block is A(wrt to ground) and the small blocks is a(wrt to the big block).
Then,
how do we decide that in which direction will the big block move wrt to the ground. We notice that the contact force N2 on the small block is unbalanced. So, there must be some balancing force so as the keep the block in horizontal equilibrium. Where does this force come from? From the given situation, obviously, only the pseudo force due to the motion of the big block will act and will balance N2. So for the pseudo force to act to the left, the big block must move to the right!
So we get the following set of equations:
T - N2=4mA
T+N1+4mg=Ng
N1=mg
T+mA=ma
N2=mA
mg-T=ma
Solving we get the following relations,
T=5mA
6mA=ma => A=a/6
Now,
mg-T=ma
mg - 5mA=6mA
mg=11mA
A=g/11
a= 6g/11
Edits: Accelerations are now according to the frames in which they were calculated.
 49
49We did not need that method anyway...
But I did by that method just to make you familiar to "How strong tools we have acquired, but never used, really are!" :D
 1
1i solved this by ashish`s method,but i think subhomoy da`s method is great.havn`t thought of applying cnsrvtn of momentum ever in these sums.
 49
49My solution:
Concepts used:
1) law of conservation of linear momentum.
2) net work done by tension=0
2) Fex=m.a
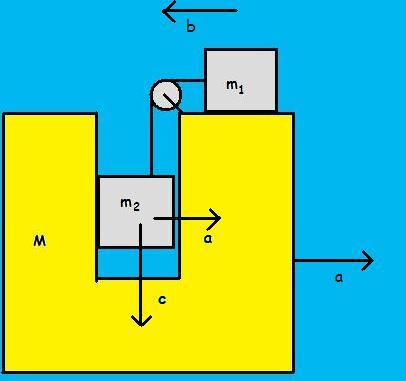
P.S. all accn are with respect to inertial frame of reference.
Let the velocity of the 3 masses m1, m2 and M at the given instant respectively be v1, v2 and V.
Next, the masses m2 and M move in horizontal direction together...
thus, V=v2
And also, net force in horizontal direction on the system comprising of all the three masses and the string = 0
thus, momentum can be conserved.
so, 4mV+mV-mv1=0 (initially everything was at rest)
thus, 5V = v1
differentiating once w.r.t time we get,
b=5a.
Next,
using constraint equation on string,
work done by tension on m1=T.xb
work done by tension on pulley in horizontal direction=T.xa
work done by tension on pulley in vertical direction=0
work done by tension on mass m2=-T.xc
thus, T.xa+T.xb-T.xc=0
gives, xa+xb=xc
differentiating twice w.r.t. time,
a+b=c
or, 6a = c
Thus,
T=m(5a)
mg-T=m(6a)
adding,
mg=11ma
a=g11
b=5g11
c=6g11
net accn of block m2= √37g11
 1
1u said u r more interested in fbd and acceleration relations...i gave both[3]...+bonus equations(6 equations in 6 unknowns==>perfectly solvable)...now i m wondering wats left in this problem???LOL!
i miss TWO pinks[3][3]
 30
30Thats a mistake. a is the acceleration of the block with respect to the bigger block!
 49
49but u already mentioned that a is w.r.t ground?? [12]
 30
30Actually in the ground frame my equations should've have been in this form:
N2=mA
T=m(a-A)
 30
30Yeah right. I made a mistake. In the ground frame, after the system is released from rest, the block moving horizontally will have the acceleration (a-A) and the block moving down will have two components of acceleration.
 30
30Hmm.. wait let me analyse again!
 49
49then the two lighter blocks do not have same acceleration in ground frame..
 49
49@Ashish: accelerations are with respect to ground?
 1
1i deserve a few more pinks[3][3]
 62
62Is there any gap between the walls where the bloc km2 is lying?
The answer will depend on that
 1
1ab had ho gayi hai...
6 equations in 6 unknowns dikh raha hai mujhe to!
 1
1its 4mA[3]..edited..bhavnao ko samjho[1]
 49
49last wala relation sahi nahi hai..
achanak se 4mg kahan se aa gaya??
 1
1edited i hope now it is corrrect!
 49
49ground frame se dekho:
T is the only force on M towards right
N2 is the only force on M towards left! [43]
 1
1btw A is the accelration of BIG BLOCK from GROUND FRAME
 49
49If N2=T
then mass M has 0 acceleration!
Check kar! That is wrong!
That makes A=0
That makes, N2=0=T [3]
 1
1Frame:BIG BLOCK's FRAME
a=accelration of small blocks
A=accelration of BIG block in GROUND FRAME(assumed towards RIGHT)
T+m1A=m1a
N2=m2A
N1=m1g
m2g-T=m2a
NE=N1+4mg+T
N2+4mA=T
 49
49that is right!
(I have a feeling that u have disregarded pseudo force but u r on an accelerating frame) [12][6]
I have this feeling even before seeing ur solution [3]
 1
1Relation b/w accelerations
From BIG BLOCK's FRAME:
acceleration of m1 towards left=accelration of m2 downwards...that's it!
 1
1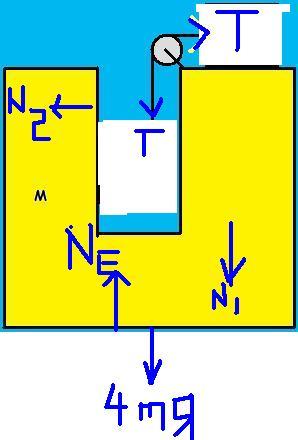
i think this is the only fbd u wanted[1]
 1
1i want some clarification before finalising the solution
are all surfaces frictionless?