21A geometry box i guess...;)
A light experiment would do but that's not allowed
A very old problem which i saw somewhere and dont think we have discussed it here before...
Given the drawing of a parabola, try to find the focus.
Nothing is given, no grids nothing. Just the parabola on a blank paper....
-
UP 0 DOWN 0 0 20
20 Answers
49This involves three steps:
1) Locating the axis.. by some property of parabola..
2) Thus finding the vertex and tangent on vertex..
3) Hence finding the focus by some other property!
We can also find out directrix easily after that..
21
21@Ricky Red line is parallel to the axis, we will draw perpendicular to the red line, it will be perpendicular to the axis [1]
1Actually , I was stuck at this point only , and like a bad student , I was not attentive enough to listen to Nishant Sir when he discussed this in class .
1" When chords are perpendicular to the axis " :
Nasiko , if you don ' t know the axis , how come you are able to draw chords that are perpendicular to it ?
21next part :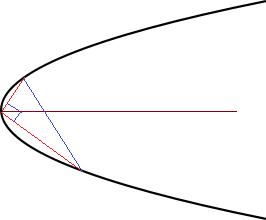
From the vertex we draw two rays which are at right angle. The intersect the parabola at two distinct points.We join this two points (blue line).This line intersects the axis at a point which is at a distance M from the vertex. We take a point on the axis at a distance M/4 from the vertex , this is the focus...
21
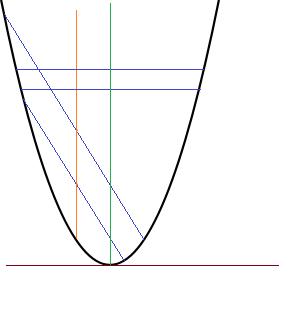
The fact is that (which i did not know) the locus of the midpoints of parallel chords of a parabola is parallel to the axis.(the orrange line) When chords are perpendicular to the axis, the locus of their mid point is the axis itself (the green line). So now we have the vertex and tangent at the vertex.
62This is one question which cannot be solved without knowing parabola inside out and having solved a few good questions!
What subhomoy has written is perfect.....
I guess this will go to the classics.
21ok. pls do not post the answer today. i will revise parabola and try it again..btw
everyone except nishant sir is allowed to answer
62Eyes are not good enuf to find the vertex :P
Had it been a square.. u would probably have the liberty ;)
21that's what i was thinking ..u wont allow us to draw a tangent..
btw do u allow me to figure out the vertex of parabola ? i have good eyes..
1then i think the method may be.....
first,drawing the tangents at diff pnts on th parabola and normal to them and then
drawing parallel lines thru the ponts on the parabola....the reflections of the lines about the normal will meet at a pnt.that is the focus.
1do v hav to find the co-ordinates of the focus by assuming an eqaution or give a logic on the location of the focus?