1yes...after studying the concept i vill try it...
Maxima Minima.
Among All quadrilaterals of Perimeter P, which has the highest area..
* Prove.. It is a square.
-
UP 0 DOWN 0 0 21
21 Answers
1i ve come across d same q before a week.......... but cant remember where i saw it...... ll search n get u d ans......
62parul.. could u try to see the full equation
or more mathematically.
cos there are 4 variable sin teh first equation
s1+s2+s3+s4=constant
area=(some function fo s1,s2,s3,s4) which needs knowing more than the sides...
could u post the formal solution parul.. so that i get ur point?
1why is that not possible?
As perimeter of quadrilateral is given.
Also let its area.
then put the value of first equation in second.
Then differentiate it.
Finally we got that x=y means both the sides are equal.
Then proved.
1Its easy to prove through concepts use in maxima &minima unit of class +2.
I am right na ?
62
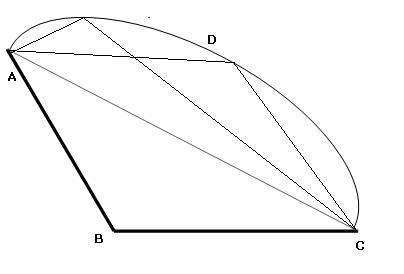
i have fixed two sides on the bold line
AB and BC.
Because the sum of 4 sides is constant.. the sum of AD and CD is constant..
so D will lie on the ellipse shown above ..
the max area will thus be when AD=CD
62I think they are angles.. but dont worry about that solution..
look into my hint
Hint:
fix 3 ponts i mean 2 sides. And then proceed.
This will really go a long way.. this question I had given specifically for a brilliant proof .. that does not in some way depend of anything else but logic! :)
62actulaly gautham.. u dont need to study ellipse.. there is a much simpler solution!!
I mean dont get confused by the talk between me and rohan.
Hint:
fix 3 ponts i mean 2 sides. And then proceed.
62yes.. so what u can do is take different ellipses on each side!
my method i used used to fix 3 ponts to get rid of this problme..
1but there is one problem
then we are taking sum of two sides on both the sides of axis equal!!
62well not exactly i meant we are fixing 3 points
We are fixing 2 lines...
I din get how u were able to make ur conclusion so easily! (givn that 2 ponts are fixed!)
1yes i got it
if we fix two points and take other two points on the opposite sides of an ellipse then also we get the solution
62hmm.. i see ur solution.. i have something much more natural..
no formulas so to say...
Yes u have done a good solution..
I will give some kind of a hint..
Fix 2 sides! then for these try to maximise the area!
1the area of a quadrilateral (just memorize it) can be expressed as
√((s-a)(s-b)(s-c)(s-d)-abcdcos2(A+B/2)
the second term is always positive
its minimum will be when cos(A+B/2)=0 (doesnt affect the values of the sides)
hence we get A+B=180
hence the expression just reduces to
√(s-a)(s-b)(s-c)(s-d)=Q
applying A.M >=G.M
s-a+s-b+s-c+s-d/4>=√Q
but 4s=2 * perimeter =2P
and a+b+c+d = P
so√Q<=P/4
equality is attained when all the terms are equal
i.e. s-a=s-b=s-c=s-d
hence we get a=b=c=d and as A+B=180 we get it to be not a square
62Gr8 work.. (I wont ask the solution..)
Only thing is that the prooff is far far easier than it might seem!