11integration mein ek point se koi farak nahin padta if that point is an end point
and do remember this also
IF A FUNCTION CONTAIN POINT DISCONTINUITY THEN ITS AREA REMAINS THE SAME
*Edited
1
(7-12x+4x2)(1+e3-2x)
integrate the above in the limits (0 to 3)
-
UP 0 DOWN 0 0 24
24 Answers
1111SIR PLEASE CHECK #14,17,19 AND PLEASE DO EXPLAIN WITH SOME CLARITY WHAT KAYMANT SIR MEANT[7]
66This integral does not exist. To be more precise the integral does not converges.
11IF U R CONTRADICTING SKYGIRL THEN SHE REPLACED X WITH 3-X
SO THE SHE IS TAKING IT AS END POINT
4 MORE INFORMATION REFER TO #14 1ST POINT[1]
13but even in the ques in post 1 the discontinuity is not a point 1 then.....
11HERE THE DISCONTINUITY IS NOT A POINT DISCONTINUITY
THERE THE DISCONTINUITY IS NON REMOVABLE DISCONTINUITY AS AT X=∩/2 TAN X MOVES UP TO ∞ AND FROM LATER IT STARTS FROM INFINITY
U CAN CHECK FROM ITS GRAPH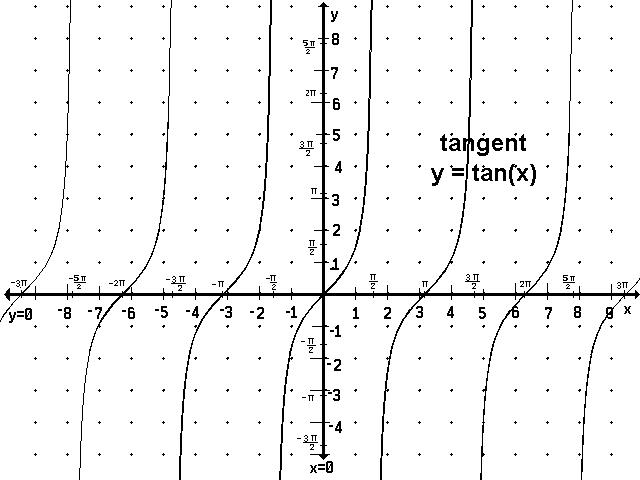
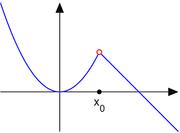
11TAKE THE EXAMPLE OF THIS GIVEN CASE
ITS AREA FROM 0 TO P( WHERE THE CURVE CUTS +VE X AXIS) WILL REMAIN SAME WHETHER THE DISCONTINUITY AT X0 IS PRESENT OR NOT
1without putting limits the ans is
[-1/26(e17+1)] log(x+7) +[ 1/13(e4+1] log(2x+1) +[1/68] log(e3-2x+1)
plz tell me whether it is right or wrong
11@ DEEPANSHU
PLEASE DONT TELL US WHAT U THINK
GIVE US THE FULL FLEDGE SOLUTION TO THE WHOLE PROBLEM
13no i think linits shud b broken at the point where denomintor bcmz 0...
1yup ans : 1/4√2 ln|(3/2-1/√2)/(3/2+1/√2))
i think simplifying, it will be same as celestine's....
1this one is exactly same as my doubt a few days ago....
jus replace x by (3-x) .
then add.
we will get ...
2I = 0∫3 dx/(4x2 - 12x + 7)
9also this q is wrong , see the denominator bcums 0 at some pt