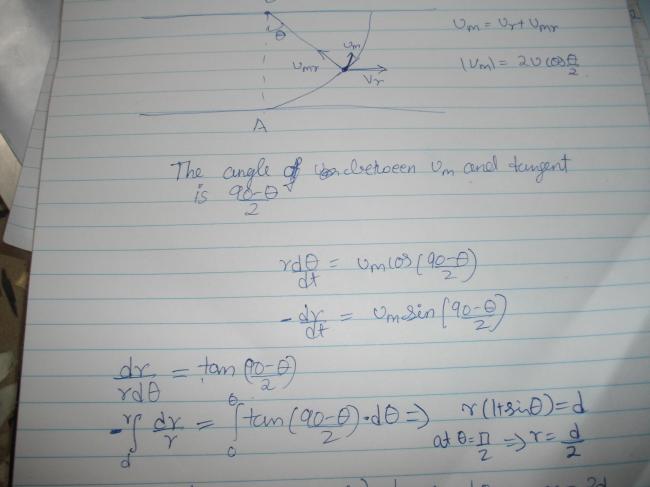1a purely mathematical proof :
Vm = man's velocity (w.r.t. stationary frame of reference viz. ground)
Vw = river's velocity (w.r.t. stationary frame of reference viz. ground)
Vmw = man's velocity w.r.t. the river.
Given, |Vmw| = |Vw| = v
width of the river = d.
Neglect, viscosity etc.
1) 
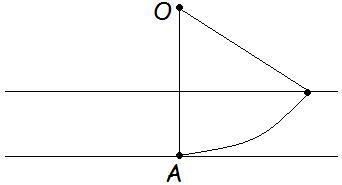
There is a point O at a distance d from the bank.
The person starts swimming from point A (given in figure) in such a way that it's distance from O is always constant.
Find time taken to cross the river (in terms of d and v).
2) 
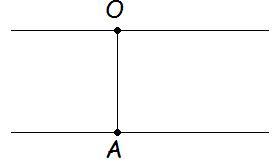
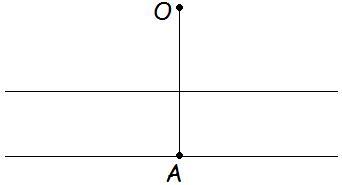
A and O are two directly opposite points, on either bank of the river.
The man starts from A in such a way that Vmw is always directed towards the point O.
Find:
a) The trajectory of the path taken.
b) The distance from point O of the man when he ultimately crosses the river.
-
UP 0 DOWN 0 0 23
23 Answers
1well clearly in second case its follwoing a parabolic trajectory as far as i can see[1]
1an ms-paint version :P
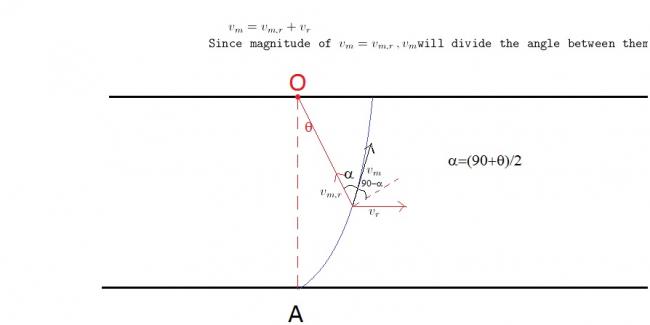
\texttt{The component of man's velocity along radius is responsible for } \\ \texttt{decrease in radius} \\ \\ -\frac{dr}{dt}=v_{m}\sin {\left( \frac{90-\theta}{2}\right)} \cdots\boxed{1}\\ \\ \texttt{The component of man's velocity along tangent is responsible for }\\ \texttt{change in }\theta \\ \\ r\frac{d\theta}{dt}=v_{m}\cos{\left( \frac{90-\theta}{2}\right)} \cdots\boxed{2}\\ \\ \texttt{Dividing both equations} \\ -\frac{dr}{r}=\tan{\left( \frac{90-\theta}{2}\right)}d\theta \cdots\boxed{3}\\ \texttt{Integrating both sides with proper limits} \\ -\int_{d}^{r}\frac{dr}{r}=\int_{0}^{\theta}\tan{\left( \frac{90-\theta}{2}\right)}d\theta \\ \texttt{We finally get} \\ r(1+\sin\theta)=d \\ \texttt{At }\theta=\frac{\pi}{2} \\ \boxed{r=\frac{d}{2}}
49Absolute Anand absolute! :D
Waise I knew it! :P
Anyway, officially welcome back! :D
491)
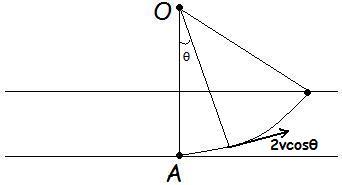
v = rω
2vcosθ = 2d dθdt
or,\;\frac{v}{d}\int_{0}^{t}{dt}=\int_{0}^{\frac{\pi }{3}}{sec\theta d\theta }
Gives answer: t=vd log(2+√3)
1tht is the picture at t=0 which u have drawn aditya...
now draw the picture at say t=5 second based on the condition that man's velocity is directed towards O...hope u got what why the velocity is not same throughout.
But yeah at every point NET velocity would bisect the angle b/w velocity of man and velocity of river by simple rule of vector algrebraic summation of two vectors[1]
262
in the second case, why is the velocity changing ??
velocity is same throughout so isnt the path supposed to be str. line ?
1btw here's something to admit at TIIT...this is Anand for those who remember me.
And for those who asked my JEE results few days(days?or a month [3]) back but i did not reply here's the reply(actually i was really feeling [2]ashamed[2] of myself for not clearing it even in the second attempt...so did not want to reply[3]):
I failed[2]..tht too really badly not clearing the Chemistry cut-off!
1Now can u say at what distance from O would the person end up on the other bank of the river?
since in the post above we proved that it is a parabola so the man would end up at a point on bank where his distane from O and our constructed line is equal(WHY? since e=1 for a parabola)
so,man would end up at a point at a distance of d/2 from O on the other bank of the river when he crosses it[1]
1well trying out a GEOMETRIC CONSTRUTION[3] to make things clear.
construct "a line" at a distance d from the man along downstream.
Wondering why?read on,things will justify themselves soon.
At t=0. Man is at a distance d from O and from our line too
At any time t,Man's distance from O and our line would be same since the velocity of man directed towards O=velcoity of man downstream.
so,by now most of us would have got it that the line we constructed turned out to be the so-awaited directrix of parabola(since eccentricity=1) and O is the focus.
Hence we have proved that the trajectory is a parabola[1]
1i am not able to solve the second
i am getting
x=v∫0t(1+cosθ)dt
y=v∫0t(sinθ)dt
49Radius is 2d...
It is moving > π4
Silly mistakes ruin everything! :(
21no it is moving Î 2 radians, that's why length of arc is Î d2
btw , is my expression correct ?
21plz tell my mistake for the first one..
the man has to move in a circular arc of length Î d2. At any time t if he covers a distance 's' (in the circular path) it's velocity will be 2vcos sd
(dsdt) = 2vcos sd
ds secsd= 2vdt on integrating you get infinite time...
49:P but here vm is changing all the time..
Anyway, give answers in terms of v and d..