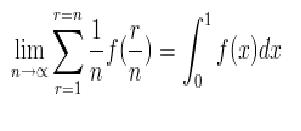b'coz its a diverging series!!
This is a simple one... if you dont get scared
Prove that
1/1 + 1/2 + 1/3+ 1/4.....
this sum is not finite.. (as n goes to infinity)
-
UP 0 DOWN 0 1 9

9 Answers
There was a kinda theorem I don't remember whose.....
The theorem stated that for a decreasing sequence....a necessary condition for its convergence is limn→∞n.un=0.....
Which is not the case over here.....
ln(1+x)=x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-...
\Rightarrow -ln(1+x)=-x+\frac{x^{2}}{2}-\frac{x^{3}}{3}+...
putting x = -1,
we get
-ln(0)=1+\frac{1}{2}+\frac{1}{3}+...
since -ln(0) tends to ∞,
the series is divergent
Shreyan, when Newton came up with this formula he specifically enjoined on all mankind to use it only when y>-1.
t(r) = 1/r = (1/n)/(r/n)
So lim(n→∞)Σtr(r=1 to n) = ∫dx/x (from 0 to 1)
= lnlxl from 0 to 1
= -ln(0)
= ∞
No guys something much more basic and simpler that these proofs!
somethgin that you can explain to a class VIII guy?
Hint:
Think of the series
1/1 +
1/2+1/2 +
1/4+1/4+1/4+1/4 +
1/8+1/8.. 8 times
and so on...
.....
.....
and then compare this with the original series...