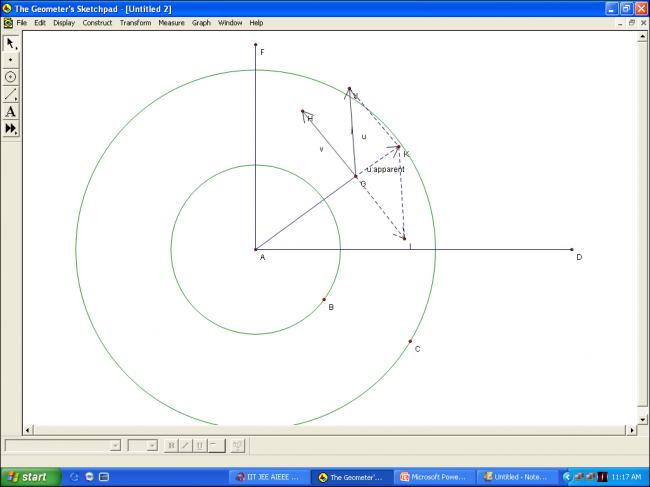
as ucosθ=v
so ucosθ+v=2v
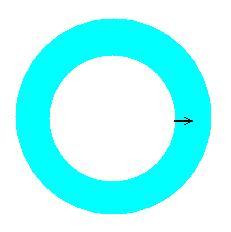
Water flows in a circular path as shown.. the speed is such that it flows at a constant speed "v" throughout the width of the river.
What is the position of the swimmer who swims perpendicular to the water flow at all times with velocity "u".
The inner and outer radii are R1 and R2
-
UP 0 DOWN 0 5 28

28 Answers
actually we evne know tangential..
so to me the distance travelled across the arc is found by taking time to travel across the stream times the velocity across the tangential direction! (Am i making some mistake?)
The only difference in ur and Rohan/IthPower's solution is that u have taken velocity of the man in still water. while they have taken it as the velocity in absolute frame.
:)
Ur work is equally commendable :)
Well done :)
Good question.
I will look at the question of the days now..
Thanks nishant, Rohan and Ith Power
sorry for deleting that post..
basically i will give another reason why it is wrong..
see the thing is that .. if u made a movement theta at a smaller radius along the tangent... and no tangential motion later on..
then only radial motion will change the distance along the tangential arc! isnt it?
So my method was totally incorrect..
Good work both of u :)
@""actually we evne know tangential..
@so to me the distance travelled across the arc is found by taking @time to travel across the stream times the velocity across the @tangential direction! (Am i making some mistake?)""
actually arc length is given by
a∫b√(r2+(dr/dθ)2)dθ
we may use it to find path travelled
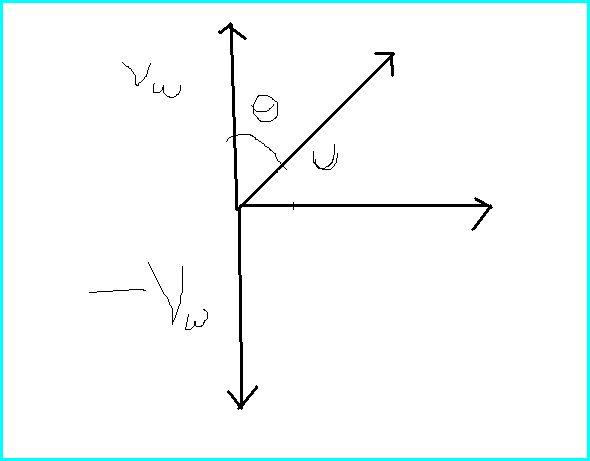 as it is given that velocity of the man will be perpendicular to the water frame
as it is given that velocity of the man will be perpendicular to the water frame
Vmw = radially outward dir.
hence
Vm - Vw =radially out ward
now see the figure
at every moment of time his tangential velocity is 2v
but his distance from the centre is changing continuosly
so the equations of motion would be
rdθ/dt(tangential velocity) = 2v
and dr/dt= √u2-v2
dividing the two equations
rdθ/dr=2v/√u2-v2
hence dr/r=(2v/√u2-v2)dθ
hence the solution follows
can you explain it rohan.? see, v is always tangential to any circle drawn with radius r from the center, so u will be always in radially outward direction isn't it?
i think the motion should be spiral. now at any moment, v is only tangential velocity, and u is radial.
actuall his speed is perpendicular to the water in the water frame
so we get ucosθ=v
usinθ=√u2-v2
speed in tangential direction = 2v
speed in radial direction = usinθ = √u2-v2
no i dont think so..
unless i am making a stupid mistake..
there is one slight obsevation i made (and this question is my own brainchild.. so sorry if the thing that i am thinking is not correct... i dont see why it should not be correct though!)
See the thing is that there will be 2 directions ofthe motion of the person..
one is radial .. one is tangential...
radial we know.. we need to find tangential!
Is this hint any useful?
what was ur thought process?
but isn't dr/dt=u, since he always swims in radially outwards direction?
dr/dt=u rdθ/dt=v, T=(R2-R1)/(√u^2-v^2).
0∫θdθ=0∫Tvdt/(R1+ut)
θ=v/u(ln((R1+uT)/R1)).
is it correct?
Time to swim across will be : (R2-R1)/(√(u2-v2)
But how did u get the other terms in ur expression?
when he reaches the other side his angular position will be θ such that
θ=ln(R2/R1)*2v/√u2-v2
hey but the river will take him to one side.. his flow is perpendicular in water frame (Sorry not to have mentioned that!)
You can take teh initial position of the swimmer to be (R1,0)
Once he reaches the opposite bank, what will be his position?