24hmm..maybe sir only can clear the air now..[1]
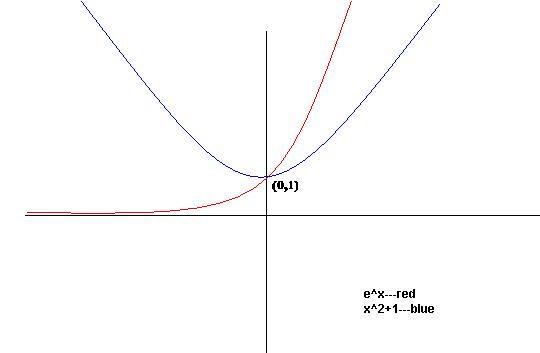
ex=x2+1
Solve this one rigorously. I dont want any short cuts or half attempts.
Ideally this could fit into Graph of the day section.. But I thought that this is not a bad place either.
-
UP 0 DOWN 0 3 30
30 Answers
1I agree with eureka (only one soln.)
definitely it can have only odd no. of solutions.
but here only one.
sorry for my previous posts i was in a hurry.
24thats the same thing .. i wrote in post#4...
why was it rejected then ??
62What I would call a routine proof: (after the great proof by prophet sir :)
at x=0 both ex and x2+1 are equal
the derivative is
ex-2x
i need to show that this is greater than zero for all x>0
at x=0, this is 1
we try to find the minimum value of ex-2x when x>0
its derivative is ex-2 which is zero at x=ln 2
the double derivative is ex which is +ve
hence x=ln 2 is the point of minima.
the value of the function ex-2x at x= ln 2 is 2- 2 ln 2 which is +ve
hence the function ex-2x is always greater than zero for x>0
hence the originial function is a strictly increasing funciton.
Hence the value is always greater than zero....
62Can I ever say no to a prophet sir's reply :D
@ sankara :
our problem is to find a positive root for f(x) since for negative x we can do it by graphs ,and f(x) is a polynomial which has a root only at x=0 and no other positive roots.
Why is the second part obvious? "which has a root only at x=0 "
btw this is a power series not a polynomial
3sir the proof is quite easy if we use series expansion na.as we are familiar with exponential series.
341My attempt: We need only look for non-negative solutions as RHS≥1
It is known that for x>0 ex≥1+x with equality occuring only at x = 0
So for 0≤x≤1,we have ex≥1+x≥1+x2 with equality again only at x =0
For x>1, we have ex>2x (easily proved)
Hence \int_1^x e^t \ dt > \int_1^x 2t \ dt or e^x - e > x^2-1 or e^x > x^2+ (e-1)>1+x^2
Thus x = 0 is the only solution
62I just want the proof that ex>2x for x >0 (edited: x/2 to 2x)
Not that this is difficult.. Only that i wanted the complete logic..
3f(x)=ex-(1+x2)
f(x)= (1/1 + x/1 + x2 / 2 + x3 / 6 + ...)-(1+x2)
= x/1 - x2 / 2 + x3 / 6 + ...
our problem is to find a positive root for f(x) since for negative x we can do it by graphs ,and f(x) is a polynomial which has a root only at x=0 and no other positive roots.
so f(x) has only one root.
21well in that q it was 2x here it is ex tat makes a difference....only 1 soln for sure
1That post was one of the best that I came across while digging through the past posts.
62Yes it does remind me of http://targetiit.com/iit-jee-forum/posts/how-many-times-63-838.html
Not to say that that it has teh same solution..
But I remember that post because the question clean bowled me :D
1This question reminds me of these bookmarks of mine.[1]
http://targetiit.com/iit-jee-forum/posts/similar-to-aragorns-34-how-mnay-times-63-34-1170.html
http://targetiit.com/iit_jee_forum/posts/how_many_times_63_838.html
24Ok not always...but b/w e^x and x^2 +1 ..e^x will always have greater value...
and why did u stress on "" rigrous "" ??[12]
IS there some trick in it ?
62none of your arguments is even half correct...
eureka.. does it always rapidly rise??
what about x^3 and e^x when x=-1?
24how ????
exponential functions always rise rapidly than any otehr ..
1@eureka how could u conclude that ex >x2 +1
if u differentiate the functions
u will find ex < 2x afer some x
and hence after some time we will get another intersection
please correct me if i am wrong
24ya only 1 soln....
becoz for x>0,ex>x2+1...so no chance of any intersection
