If I am not mistaken,this is the most controversial question in the world of mathematics...........It involves the number of infinite reals b/w 0 an 1...................I wolud not like to answer this question.......But I would want that everyone should read this page.......http://www.ii.com/math/ch/.....
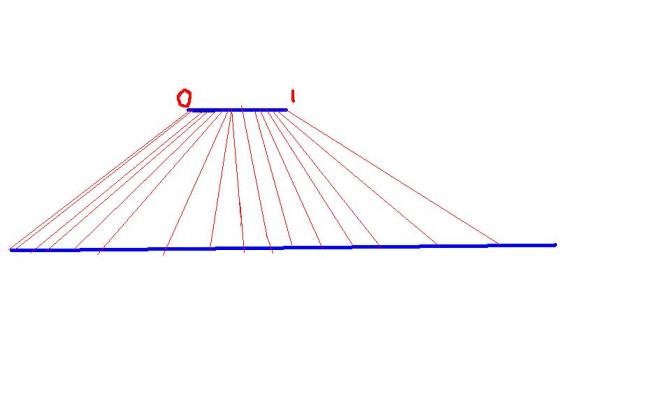
Give a one one onto relation between (0,1) and R
Does this prove that the number of Reals is same as the number of numbers in the interval (0,1) ?
-
UP 0 DOWN 0 0 12

12 Answers
Quantum hypothesis:Any set of real numbers is either countable or can be put in one-to-one correspondence with the entire set of real numbers.
yeah it depends upon our realisation we can assume it either to be equal or unequal.
i preffered unequal cos of the range difference
have u seen that link????just go through it and u would know how big this question iss!!!!!!!!!!!
yes i saw that ..........
its jus a hypothesis u need not go by that trust ur inner feeling thats all
i jus managed to covince myself that they r unequal so wont change my idea ;)
log (1/x - x) for x > 0
but we can not compare infinity. if we able o compare infinity then it will lost its existence.
in my opinion we can not say that nos of real are same as nos in (0, 1)
actually there r infinite reals between any 2 no.
for example between 5 and 5+h ;where h is very small;
no one can count it ;(bcoz there r infinite no.s)
THen only foolish ppl talk about comparing it(except us :D )
There is no question of cmparing something which we cant count;
10100 viruses will cause u same problem as 101000000000000000 viruses;
i hope u understand my feeling;
guys there is a one one relationship..
I understand that celestine and mkagenius dont appreciate this fact right now..
But atleast the good thing is that celestine did give a good one one onto relationship :)
how should we get the relationship that celestine got
i mean how can we check if it is oneone onto