3neclues for us sir.
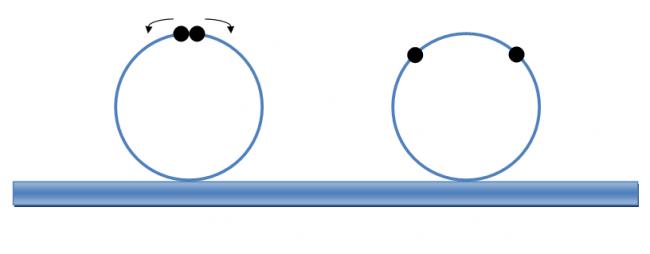
The system above in the diagram iis released.
The mass of the black beads is m, while that of blue loop is M
What is teh minimum m/M ratio needed for the lower loop to take off from the ground..
(A variation of this question was in FIITJEE GMP long time back... I havent seen the latest one... )
-
UP 0 DOWN 0 1 10
10 Answers
3i think asish u have done by applying force eqn.
N-2mg-Mg=0 if N=0 we get m/M=-1/2 which is not possible so i think nishant sir want us to think more.
66This and many more problems, you can find here:
http://kaymant.googlepages.com/101ProblemsInMechanics.pdf
(It was supposed to be a collection of 101 problems, but so far contains only 94 of them.)
62That is an awesome set of questions :) Each one seems to be a gem :)
I hope you are able to complete the 101 soon..
btw what;s with your book? found any publisher?
We have plans of publishing a book.. wanted to talk to you about our own progress... but we havent been able to meet.. last time rain Gods din want us to :D
66I had talk with a few publishers. And the talk didn't go the way I would have liked. They wanted to have full control over the presentation, but I wanted it my way. I am considering publishing it myself with the print-on-demand technology. I had plans of publishing it around december or so... but it seems that it will take a bit longer --- around march.
62Yeah the publishers want everything
even our magazine plan took a back seat because of that :(
they want too much controll....
1(at any instant at an angle θ )
for bead;
N+mgcosθ=mv2/r -(1)
and using COE =mgr(1-cosθ)=1/2 mv2
v=√2gr(1-cosθ)
now putting in (1)
N=mg(2-3cosθ) -(2)
now for 2 beads the upward force
F= 2Ncosθ=2mgcosθ(2-3cosθ) (from (1))
to get the θ for which this upward force is maximum ,we defferentiate the eq
d/dθ (2cosθ-3cos2θ)=0
we get cosθ=1/3
so upward force = 2mg/3
the hoop will rise if 2mg/3>Mg
m/M>3/2
is it correct sir