Yes there's a symmetry occurring for both the cases which leads to this answer.
Q1 . 2 symmetries
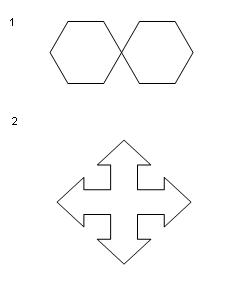
Q2. 4 symmetries.
Got this idea after one of sinchan's posts...
Not worth a QOD.. but still a nice variation of Seating arrangement.
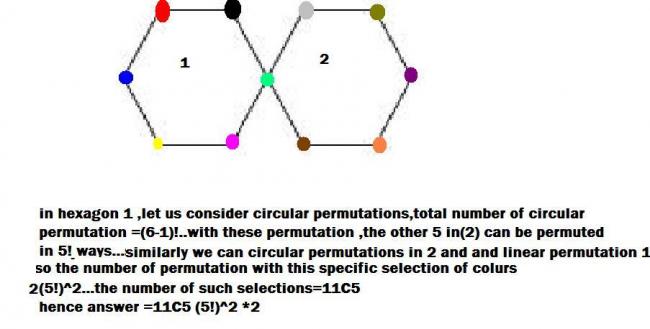
What is the number of ways to seat people at each of the vertices in both the images below.
Aside: I will try to bring the QOD section back on after december
-
UP 0 DOWN 0 2 17

17 Answers
2) we can seat the people in 24! ways
but when we see carefully, we see that when we see the arrangement from botton top right and left it gives the same arrangement
so ans is=24!/4
for q.1>> no. of ways=(5!)2[ considering both hexagons as identical]
no not even then :P
* btw now i understand your logic.. and you have made the same mistake that i was thinking that ppl would make [1]
there are 2n-1 seats...
n-1 on each ring and one in between..
I did not get your logic... but I dont think that answer is correct