1plz chek the link given by tushar...there are quite a few unanswered doubts in dat post
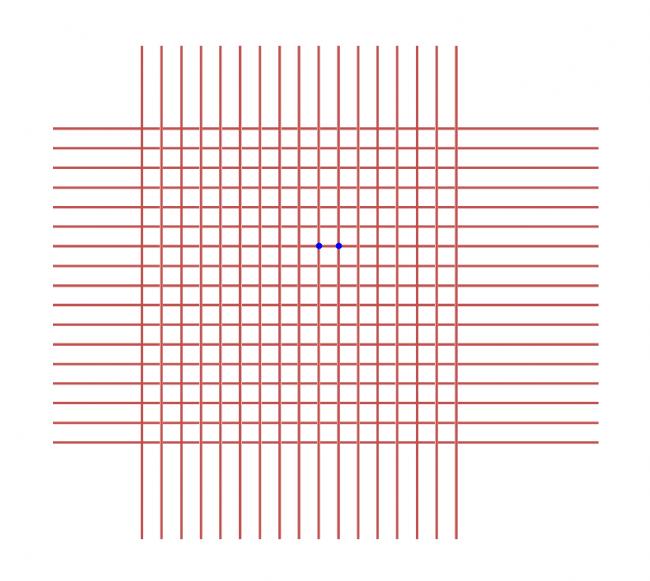
This is an infinite grid...
Find the resistance between two consecutive nodes...
PS: This is a very old question which has appeared in a lot of places including IE Irodov..(If I remember correctly)
This problem uses a trick which is otherwise not used very commonly!
Also, If i remember correctly, we have never discussed this question here!
-
UP 0 DOWN 0 1 7
7 Answers
11http://www.targetiit.com/iit-jee-forum/posts/resistance-9716.html
62So then lets look at a variant of the same question..
This is a 3D mesh now :)
1when we did it last time..it was never explainbed how the current came to I/2.......so can we plz have the explanation nishant bhaiya???
1
66For those who are interested.....
If we consider the two dimensional square grid and map it into the Cartesian plane with each node occupying a lattice point, then the equivalent resistance between the node (0,0) and the node (a,b) is given by
R_{a,b}=\dfrac{R}{4\pi^2}\int_{-\pi}^\pi\int_{-\pi}^\pi\dfrac{1-\cos(ax+by)}{2-\cos x-\cos y}\ \mathrm dx\, \mathrm dy
where R denotes the resistance of each unit of wire.
As an example, the above formula yields (correctly) the equivalent resistance between two adjacent nodes (0,0) and (1,0) (which of course would be obtained easily using superposition) as
R1,0 = R/2.
1another solution which i found while surfing :
principle of superposition:
first consider a battery whose one end is a at and another at infinity: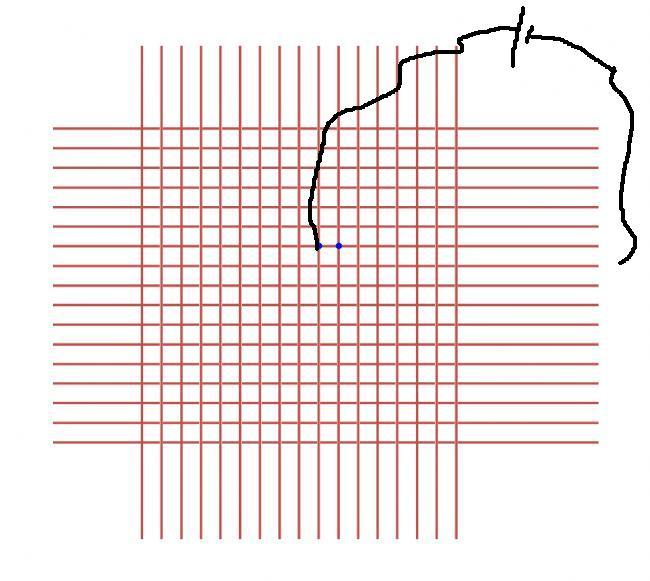
Force the circuit at point A while holding voltage zero at infinity. By symmetry, 0.25 current flows through the resistor between A and B (going from A toward B).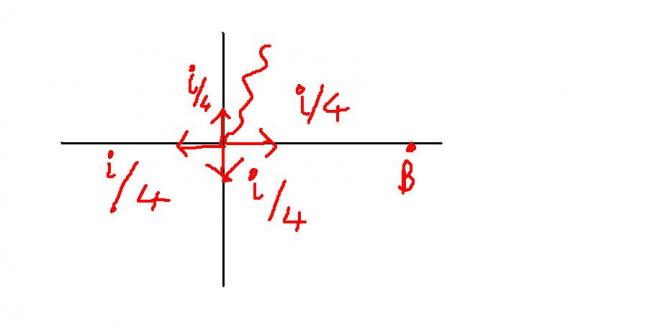
now :
Take current out of circuit at point B while holding voltage zero at infinity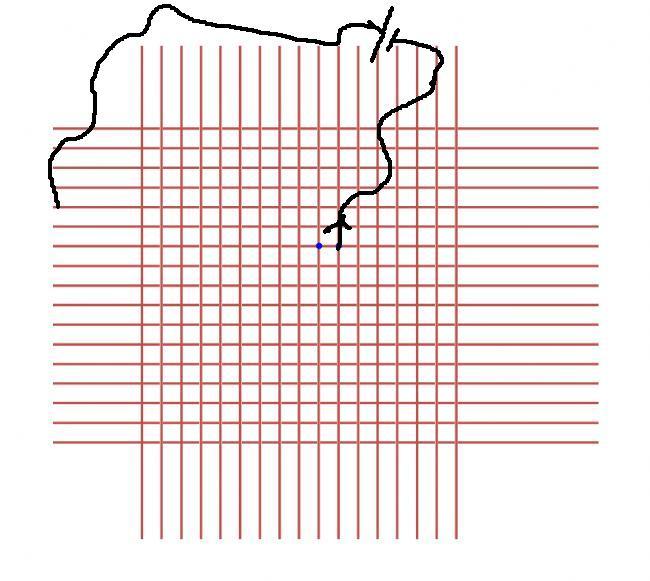
By symmetry, 0.25 currentflows through the resistor between A and B (going from A toward B).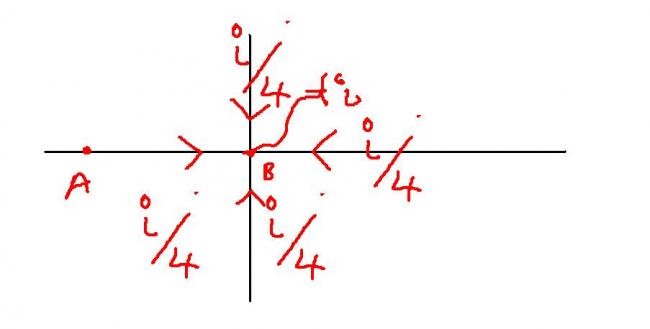
Superimposing these two situations gives 0.5 i flowing through the resistor between A and B
hence equivalent resistance R/2
62Yup this is the one i had in mind..
except before Anant sir came up with this one :D