is hte final condition OK ???
This question has appeared on an online physics site... (given by Rohan to me)
Lets have a tall cylindrical vessel filled with water (radius r, height of water h) and spin it around its axis at angular speed ω. At the centre of bottom is a small orifice of surface area S, while the vessel is still rotating. How much water will escape the vessel?
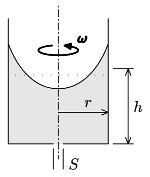
PS: The final solutions are not out.. But this is a good one to solve .. :)
-
UP 0 DOWN 0 0 7

7 Answers
I am doing like this...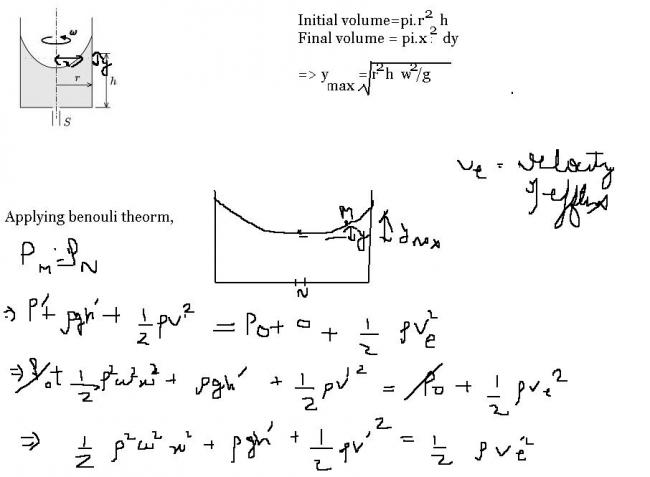
I am facing soem problem in finding h' and v'
also hte final situation means this ???
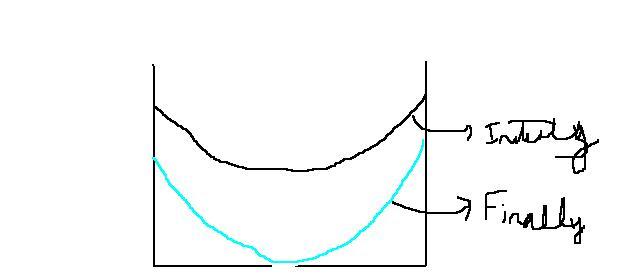
i.e vertex of paraboloid on orifice so that no more water flows out
tell me if I am on right path
I tried to solve the problem last night..
The problem i was facing is that what is the use of area.. if the area is not very small, it wil be a variable mass problem equivalent of rotational...
If it is small, we can work a solution simply.. (though there are a couple of dirty expressions taht you will encounter...)
I am waiting for someone to post a solution that uses S nicely..
What eureka has analyzed is basicallly what i have done.. only that omega will not be constant...