1well here is the proof by calculus
as already said by bhaiya its not a glorious proof as given by ith power
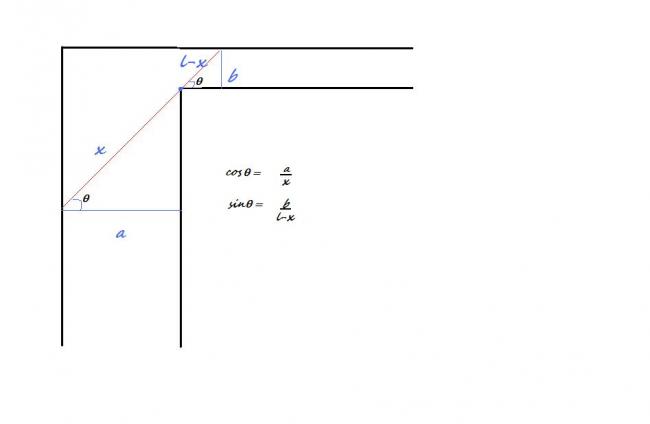
A Long bus has to be passed from the top to the wider road on the side horizontally.
The width of the road at the top= a
The width of the road at the side= b
Find the longest bus that can be made so that it can turn.
Assume: Bus is of zero width!
-
UP 0 DOWN 0 4 19
19 Answers
62how does just lying on the envelop give that answer :O
I mean it could well be that it falls in the envelope but there is a longer rod that can pass... or that this rod may still not pass!!
I mean how can u be that sure!
1
1How to do this by maxima and minima??
I am getting a slightly different answer. :(
11were do u get this geometrical sketch pad stuff? i saw it in my school math lab yesterday n i was mighty impressed.
62i understand that dude :)
what i meant what that
dont you think that we wud be better off solving it as a maxima and minima problem..
(I dont take away anything for your thought procss) but i think it will be much tougher doing the same in the exam hall!! (I mean gettting the equation of this curve! than solving the question by the less "Glorious" method!)
1the equation i used is actually equation to an astroid.
ref.= http://mathworld.wolfram.com/Astroid.html
62One thing..
how did u get the equation of the envelope? (Just for the completeness of the proof :)
62Yes wonderful :)
gr8 soln..
I was stuck with my maxima minima :)
good work :)
1
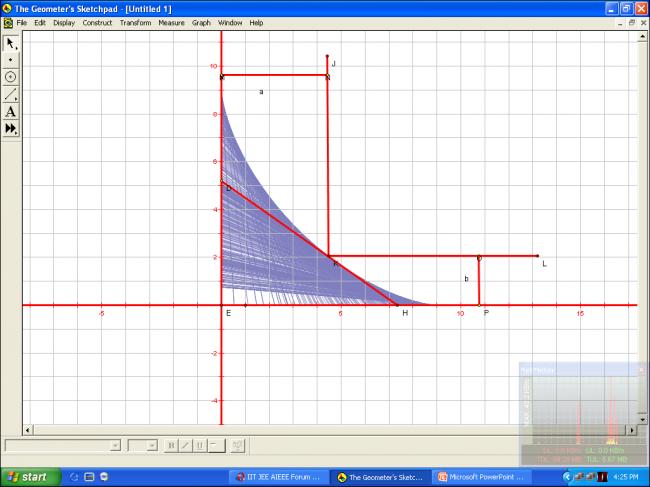
check out the picture please. if any rod larger than DH tries to pass the corner it would get stuck at 'K'. isn't it?
1i think answer should be (a2/3+b2/3)3/2, Vibhav is right..
explanation:
equation of envelope of a falling ladder of lenght l(two sides one on a vertical wall, another horizontal ) is (a2/3+b2/3)= l2/3, since, given a,b is a point on the envelope, (a,b) must satisfy given equation.
62Could you give more explanation? to your answer abhinav?
take the case when a=b.. what should be the answer?
62prashant's guesss was very very good... but not the right answer...
Anyone who cna confirm if any of these is the right answer?
