1
We all know that the path of a projectile is a parabola.
My claim is that if we threw a stone in real life (Even without air friction), it will not follow a parabolic path.
Am I correct? If yes, then what will be the path.
If no.. Think again ;)
-
UP 0 DOWN 0 0 20
20 Answers
1is it that projectile travel below escape velocity so its elliptical???[7]
62so far as sanchit has said abotu the trajectory being a conic is correct..
but after that depending on whether the speed of the stone is less, greater or equal to the escape velocity, the path will be elliptical, hyperbolic or parabolic..
Btw... humans cant throw stones at escape velocities [3]
hence a elliptic path
1sanchit
mathrmatical proof :
since the energy is -ve the path has to be closed or bound
the conic section that is closed is ellipse
y conic section ??
its because the the polar form of trajectory is
which represents a conic section
how we got this equation ??
by solving the differential equation
and
** put u=r here
make subsituition r=1u
to get this equation
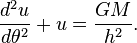
this simple harmonic motion and solution to this equation is
http://en.wikipedia.org/wiki/Orbit for more clarity
1357sorry guys my bad.. the diagram made me think that the image posted is that of the flattened earth due to the rotation of it.. [3]
So I said that that will cause the deviation..
But the explanation by sanchit (of course one needs to magnify it :D) is correct
1sanchit is right......but nishant bhaiya wanted more explanation .... :-)
and kalyan is right too .... but not the answer to why ELLIPTCAL.
@Nishant Bhaiya : Can't think of anything else.........
@archana : if the object is thrown at a vel equal to the escape velocity........it's bound to follow a parabolic path.....and other conics for other cases.
it's because of v lesser than esc. vel. that it has to return to earth else it'll go out of reach and will be touching the earth just like a parabola.
1cant understand whts mistake in ma diagram to explain this one???????[7]
6@aveek cudnt understand ur soln...
@ nishant bhaiya
d fact dat it is nt in parabolic path -if i answer dat earth isnt a perfect sphere nd g isnt same thn .....or if i proceed wid d fact dat earth isnt a perfect sphere cud i reach sumwhere???
pls ans
1sir will the second statement in #10 be "deviation from parabolic path" ? If that's so then the reason is that gravity is not same everywhere .
Why ?
because it's launched with a velocity lesser than escape velocity....it won't go out of reach of earth...gravity will be attracting.....we first conserve angular momentum of the particle about it's initial position and the highest point and then conserve energy.....that's where we come into the idea of an ellipse.
But parabola is a special case of ellipse where e=1 ..... so when gravity is same at all points the foci meet and there's only one foci......so we get a parabola in the2nd case.
62sanchit.. that is a reason.. but you are missing out the major reason...
Infact that will be the reason of why there is a deviation from the elliptical path :D
62@Kalyan.. Gravity is not the same everywhere... Why?
@Kamalendu.... Is g ka direction perpendicular in the case of a projectile? I dont think so!
1is it also bcuz.. g ka direction directly perpendicular nahin rahega and so vx will also get a retardation component of g???
so ellipse to cirlce(when velocity>escape vel) ????
6it is not parabolic coz gravity is not same evrywhere.....
can dis be a possible explanation??
nishant bhaiya pls check
62Good one.. ppl are cracking this one..
Other than Philip, can you justify
a) Why it is not parabolic (The easy part)
b) Why it is elliptical (The more difficult part)
