how how how did you know the very similar question gonna come in I.S.I????neways thanx for the question.:)
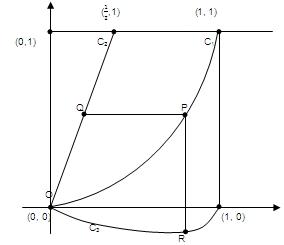
Let C1 and C2 be the graphs of the function y = x2 and y = 2x, 0<x<1 respectively. Let C3 be the graph of a function y = f (x), 0<x<1, f(0) = 0. For a point P on C1, let the lines through P, parallel to the axes, meet C2 and C3 at Q and R respectively. If for every position of P (on C1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
-
UP 0 DOWN 0 1 5

5 Answers
let p be (t,t^2)
Area OPQ=\int_{0}^{t^2}{\sqrt{y}-\frac{y}{2}dy}
Area OPR=\int_{0}^{t}{x^2-f(x)dx}
these two areas are equal.
or \int_{0}^{t^2}{\sqrt{y}-\frac{y}{2}dy}=\int_{0}^{t}{x^2-f(x)dx}
Now differentiate both sides wrt t:
\left(t-\frac{t^2}{2} \right)2t=t^2-f(t)
or,f(t)=t^3-t^2
assumed that the function is cont in the int (0,1)