mmax=Mekpi k is the friction coeff.
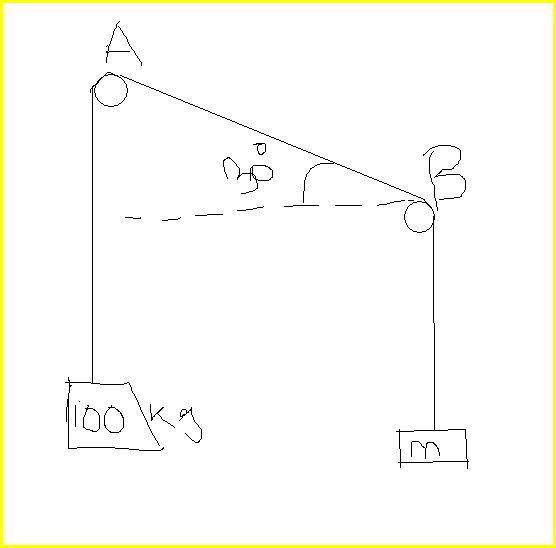
The figure shows a rope looped over two pipes A and B.If the coefficient of static friction is 0.25 in both the surfaces , determine
smallest and largest values of m for which equillibrium is possible
-
UP 0 DOWN 0 7 8

8 Answers
Letting M=100 kg, the required values of m are
m_\mathrm{min}=Me^{-\pi/4}
and
m_\mathrm{max}=Me^{\pi/4}
kaymant sir, cud u please explain how to solve problems based on pulleys with friction.
try deriving
|dT/dθ | <= μT where T is tension abt a point on the rim of circular pulley
To resolve the issue, let me show how to approach a problem of pulley with friction. The relevant diagram are shown below:
I shall assume the situation in which T1 is greater than T2 and the string is on the verge of slipping towards the left, so that friction acts towards the right (I forgot to show the friction force).
At some position measured by the angle \theta from the point of contact on the left, let the tension be T(\theta). Take a small element at this position which subtends an angle \delta \theta at the center. We see that the components of the two tensions towards the center balance the normal reaction N, so that N=T(\theta)\sin\dfrac{\delta\theta}{2}+T(\theta+\delta\theta)\sin\dfrac{\delta\theta}{2}\approx T(\theta)\delta\theta
where I have used the fact that for x<<1, sin x ≈ x.
Along the tangential direction, we have
T(\theta)\cos\dfrac{\delta\theta}{2}=T(\theta+\delta\theta)\cos\dfrac{\delta\theta}{2}+f
where f is the friction force. Since for x<<1, cos x ≈ 1, we get
f=T(\theta)-T(\theta+\delta\theta)=-\dfrac{\mathrm{d}T}{\mathrm{d}\theta}\ \delta \theta
Since,
f\leq \mu N
we get
-\dfrac{\mathrm{d}T}{\mathrm{d}\theta}\leq \mu T
In case, the string is just going to slip, the equality in the above inequality holds. In this case, we have
-\dfrac{\mathrm{d}T}{\mathrm{d}\theta}= \mu T
which gives
\dfrac{\mathrm{d}T}{T}= -\mu \mathrm{d}\theta
Integrating the above expression when \theta
varies from 0 to some \theta in which case the tension varies from T1 to T, we get the tension as a function of \theta as
\int_{T_1}^T \dfrac{\mathrm{d}T}{T}=-\mu\int_0^\theta\mathrm{d}\theta
from where we get
\boxed{T(\theta)=T_1e^{-\mu\theta}}