for solid im gettin
2a/3(7 - 2Î )
Find the center of mass.
(this question is taken(as is) from a book meriam kraige which all these fiitjee and other ppl use to LIFT their quesitons from)
Do not read this book. I will make sure you guys get all the questions that are relevant for your standard are posted on the forum.. Many many things in this book are not for JEE!
***edit***
(Question given was for a hollow thing!)
***end edit***
now, can ny one tell me coordinate of the CM of a quarter of hollow sphere,
if it can be found, this question can be solved easily
i think it is (R/2,R/2)
dude.. 2 coordinates will be zero anyway.. only z will be non zeroo..
check your solution..
no, u didn't get me,
i am talking in general,& not about this question in my previous post
& in my previous to previous post i have given z coord of CM of the body.............
i think u r taking quater hollow sphere on different axis & i am taking in another...........
i am not abs sure but i think what i got when i solved first
was a/(pi-2)
but just check once.. may be i am wrong!
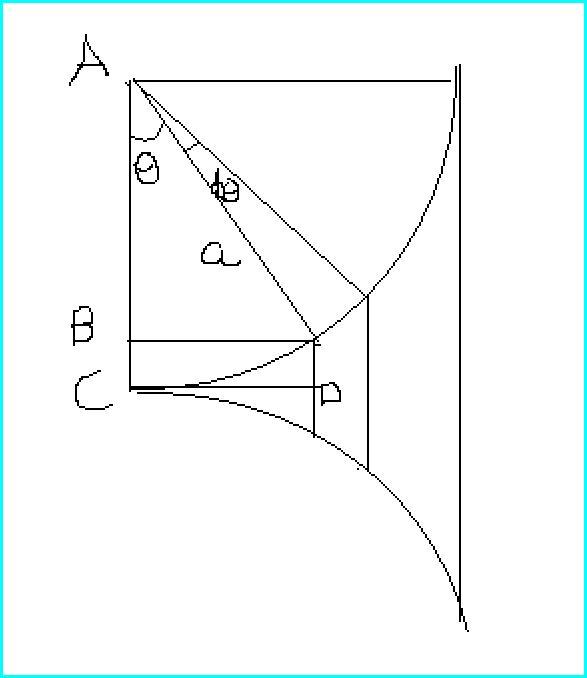
for the hollow one
see the figure
we can see that dm= 2πr* adθ (as mass is along the surface)
where r= radius of circle when angle =θ
so r=AC-AB=a(1-cosθ)
so dm= 2πa2(1-cosθ)dθ
m=2πa2 0∫π/2(1-cosθ)dθ= 2πa2[π/2-1]
further the x coordinate of centre of mass w.r.t C=
(1/M)(∫xdm)
x=CD=asinθ
and dm=2πa2(1-cosθ)dθ
so ∫xdm coordinate = 2πa30∫π/2(1-cosθ)sinθdθ
=2πa3(0∫π/2sinθdθ-(1/4)0∫π/2sin2θd2θ)
=2Ï€a3 (1-(1/4)(1-(-1)))
=2Ï€a3(1/2)
hence coordinate of com = ∫xdm/M=[2πa3(1/2)]/2πa2(π/2-1) = a/(π-2)
arey yeh wala toh main integration pe attak gayi ! :(
huh!
0∫Π/4 θtanθ dθ = ????????
..its like i am taking a samll strip of dx ..x dist from the point C(see rohan's fig) .. now this strip will make some angle θ at C.
so we have x/θ = a/(pi/4) => x= 4aθ/pi.
then taking the area of one strip like 2Πrdθ.. we integrate it from 0 to pi/4.. to get the whole area...
correct me if wrong...
well, you are assuming a linear variation between x and θ.
its actually x=a sinθ
or x is proportional to sine of the angle θ
and why x=a when θ=pi/4?
oops sorry.. it will be 0 to pi/2..
@prashant, x=asinθ acording to rohan's figure..
but my theta is different...
i found the fallacy in rohans proof
thickness is adθcosθ and not adθ
dont u agree
putting the new value you get my solution
i think even Nishant sir has don same mistake
no it wont be adθcosθ
because see the matter is along the surface not along the interior
further when you calulate the surface area of a hollow sphere what do you take that one
dont you take it Rdθ ??
no satan im veeeeeeeeeeerry sure its adθcosθ
try to put some good thought to it
u will understand
if u dont i shall explain in detail
but then you shall not be able to find the area of a sphere correctly!!
oops.. sorry guys..
i am not in this second part of the qeustion.. u guys figure it yourself :P
that is the dirtiest answer i have seen in a long long time!
ok if inside is hollow..
centre of mass lies in the z axis and at a distance of a/(Ï€-2) from the null point
Z component i am getting is: solid case
Opse Never see this
a-[(1/√2){(√2-1)-pi/4(√2a-4a√2/3pi)}/{1+pi/4}]
:P
But i have not done any integrations...
May be my method is wrong or sumthing like that