1oh, i didnt read the 2nd part, sory
If you can solve this question, I dont think you should worry too much about this chapter on a whole. This is probably everything in capacitance.
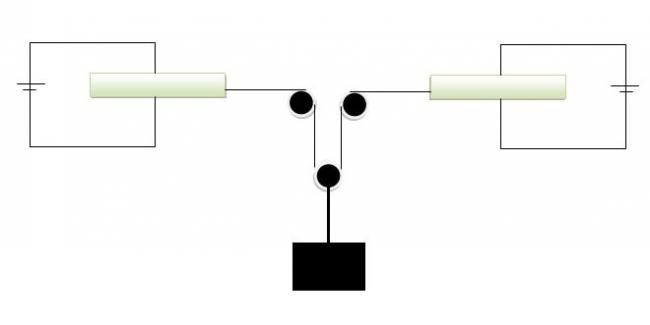
There are two smooth dielectric slabs of mass m. And dielectric constants k in between the plates of paralllel plate capacitors. The dielectric slabs are attached to the string and pulley system. Assume frictionless massless pulleys.
THe capacitor plates are with separation "d" and widht b. They are connected to a emf E as shown.
a) Find current in each circuit as a function of time
b) Find the acceleration/velocity of the masss (black) as a function fo time
(Again another problem that i thought of.. so excuse me if there si some mistake! But you should try to understand the basicss)
Dont get overwhelmed by this quesiton. This is not as tough as you may think. Just give it a shot!
-
UP 0 DOWN 0 1 11
11 Answers
1sir, is the system in equilibrium,
if yes.then there has to be a resistance in the circuit, otherwise the charge on capacitance becomes constant, ie, q = CE so, dq/dt becomes zero,
pls reply.
62The system is not in equilibrium. I have asked for the acceleration (so how can the sytem be in equilibrium ;)
1sir, my acc. of block is comming constant
a = E2ε0b(k-1)/md
& velocity = {E2ε0b(k-1)/md}t
please verify........................
1here goes the full solution
writing the constraints for both
we have accln of lower block= accln of upper slab=a
then
mg-2T=T+F
T=mg-f/3
where F force due to capacitor
F=-dU/dx
capacitance=εA/d(x/b+k(b-x)/b)
dC/dx= εA/bd(1-k)
F=-E2dC/dx
=-E2εA(1-k)/2bd
hence acceleration=
((mg-F)/3+F)/m
=mg+2F/3m
current =
EdC/dt= EdC/dx*dx/dt
=EεA(1-k)/bd*v
but v=at
so the answer follows
earlier i made a short mistake
1& current is comming,
i = {E5(ε0b(k-1))2/2d2m}t
pls. verify...........
1and @dimensions
how come u re not getting g in your answers and A = area of the capacitors?
1here A will be
A = b*l
now l is getting cancled in my solution & my ans is comming in terms of b.........
9as u dint menton mass of block i took it as m
i = εEb(k-1)at/d
a = g - εbE2(k-1)/md
dimensions dint consider g
