1
1but we can always declare a function f such that f(g(x)) is another function
and then after that analyse it
i got [g(x)]=x
which means x is an integer and
i) if x>0
g(x) >=x<x+1
that means we will get infinite values of y for a value of x!!
that means that
that stament is always right
that proves that g(x) doesnt exist!!!
 1
1a relation X-->Y is called a function when there exists a unique image for all x belonging to X.
since g(x)=f-1(x)
gives infinite real values for any x.
it is not a function
 1
1f-1(x)=g(x)
that gives
f(g(x))=x
but f(x)=[x]
so
[g(x)]=x --- (i)
that gives x should be an integer
that means is inverse will be defined for all integers
further
f(x)=g(x)
implies
[x]=g(x)
it means g(x) is an integer
from (i)
we see that
[[x]]=x
as x has to be an integer
the above condition is satisfied for all integers
 62
62yes philip .. you are right :)
good work.....
Now tell me why did i say no to varun's answer..??
I mean there is only a very small difference!!!
Why is varun's solution not correct...? ((not a tough one after you have cracked this part!)
 62
62Satan you tried very well.. infact a very good attempt..
but you are not bot it right unfortunately! :(
See The discussion between me, varun and the final answer philip gave...
and answer my previous one..
 1
1now the inverse of [x] wud exist if only we restrict the domain to all integers.
therefore we restrict the range of g(x) to one value per x
now for all x belonging to Z f(x)=g(x).
isn't it correct?
 1
1plz point out the mistake in my solution
 1
1Restrict the range ?! Thats the mistake ?
 62
62Satan.. you made the same mistake as varun and vibhav did..
varun.. when we define sin-1x did u ever think why we take the domain as [-pi/2,pi/2] ??
why not [-3pi/2,-pi/2] ?? or [pi/2,3pi/2] ?? or many other such possibilities??
That is becasue this is a "standard convention" you could say ppl have accepeted this as a standard definition world wide....
Coming to the 2nd part of your question... (I mean for this question)
Why could we not have taken points like 0.5, 1.5, 2.5 on the x axis??
then we would have some other answer... isnt it?
You were also restricting your domain.. but why do you have to be biased about the point you are taking as integers!!
 1
1plz point out the mistake in my soln
 1
1i have solved it differently plz see it carefully..
 62
62satan.. the problem is that the premise of your solution is wrong..
Like.. you have already asssumed that f-1 exists.. which is wrong!!
so the mistake is that assumption!
 62
62so close yet so far!!!
Good atttempt!! Infact very good.. but u are still making a small conceptual one...
 1
1what is the reason to have chosen integers then ? ( I was biased ofc ) but it can be diff for diff set of domain we take right ?
 62
62moreover, what you have proved is that .. if a solution exists, it will be such that x is an integer.. you have not proved that x is indeed a solution...
i will tell you another example for this.. (to make my point clear!!)
see you say that √x =-1
so then what you do is take square you get x=1 but √1 =1 not -1!!!
 62
62you are assuming that f-1 exists.... at the first step!!
how can u do that?
 1
1no solution?
i have a foolish reason... f(x) is a function n g(x) is not a function ... so we cant equate both of them ...
 1
1but cant be things disproved after assuming first they exist
and then if our conclusions dont allow them to
then our assumption is wrong
i.e. they donot exist
 62
62@sky
yeah basically that..
basically g(x) does not exist! so g(x) is a null net! basically undefined!
might have seemed a trivial one but i definitely caught a lot of u napping :P
 1
1the point that f-1 does not exist must have come from an earlier point
i am just reaching that earlier point
 62
62"but cant be things disproved after assuming first they exist and then if our conclusions dont allow them to then our assumption is wrong i.e. they donot exist"
Yes they can be.. but even after contradictions you might not be able to find all the contradictions... otherwise we would have done all problems by contradictions....
you must also realise that we generally solve problems which are like: Prove that no integer exists or prove that there is no triange.. etc etc..
we rarely use them for finding solutions....
 62
62dude.. either i have no clue to what you are trying to say or u have no clue to what i am or we both dont !! :P
what is your first step??
f-1(x)=g(x) {This comes from the question!}
So if something is empty there... then where is the question of takeing a composite function f() on the whole thing and making it
x= f(g(x)) ???
 62
62satan: in the first step
satan: i took the function/any mapping as g(x)
satan: then i got that if there is any g(x)
Nishant: you can take only a mapping..
Nishant: so we have a mapping g(x)
satan: then it should follow the condition that
satan: [g(x)]=x
Nishant: yeah u did get that if there is a mapping, then it will only have a solution that is x=[x]
Nishant: that part is fine..
Nishant: now?
satan: so from here we CAN deduce that x has to be an integer
satan: fruther f(x)=g(x)
Nishant: yes
satan: implies we have to find all those values of x such that they both are equal
Nishant: but then what you have proved is that for the function to exist.. g(x) must be of that form.....
satan: for that value of x
Nishant: so u have answered the question that find all possible values of g(x) for which this is true..
Nishant: you have not found the inverse of f!
Nishant: there is a very subtle difference.
satan: but here x refers to only certain allow values
Nishant: how can u say that?
Nishant: i have defined f for the whole real line!
satan: as we have not yet found g(x)
Nishant: how can u change the definitioeon of f in between the answer..
Nishant: f is defined already .. u cant touch it
satan: i am talking of g(x)
satan: simply we have to find those x for which f(x) = g(x)
Nishant: is that the question?
satan: if there exists such a value of x
satan: yes that is the question
Nishant: yeah that is .. but hen how does it prove that your g(x) is the invers of f(x)
Nishant: i have specifically defined g(x) as the inverse of f
satan: i have not applied that fact yet
Nishant: and not the fancy definition that you are trying
Nishant: i know u are trying to say something very good..
Nishant: so!
Nishant: you have to apply that at some point!
satan: yes at last
Nishant: and i totally understand and appreciate the spirito fo your solution
Nishant: so whevere or as soon as you do that.. the question falls!
Nishant: i mean the solution.. g becomes undefined!
satan: g IS undefined
Nishant: yes!
satan: but defined for certain x
Nishant: so then why are we not reaching a common agreement that ther eis no solution?
Nishant: what do u mean by that!
satan: that i have showed that x has to ba an integer!!
Nishant: it is not!
Nishant: you are confused with the inverse thing.....
Nishant: we can make inverse of functions by creating new functions..
Nishant: not by just the same function..
satan: then even integer is not the solution
Nishant: you should realise that the sin-1 function is the inverse of something less than a sinx!
Nishant: it is not the inverse of sinx as wer know that
Nishant: yes.. you are right now..
satan: you mean to say there is no solution?
Nishant: yes.. i have been saying that for long now ;)
Nishant: i hope you are convinced.. cos i have not much left in me to explain more to you ;)
Nishant: :)
Nishant: i mean i am short of ideas.. if you havent been able to understand my point!
satan: ok
Satan did not understand what i was trying to say.. but i hope this gives more perspective about this quesiton to the rest of you guys!
 1
1f(x)=[x]
g(x)=f-1(x) => g(x) = x+Δx where 0≤Δx<1 and x is an integer
f(x)=g(x)
=> [x] =x+Δx
L.H.S is an integer .. so Δx = 0. and the sol is all integers ..
Is that correct ?
 62
62yup man.. but i am sure half the ppl here will get the right soln using the wrong method!!!
 1
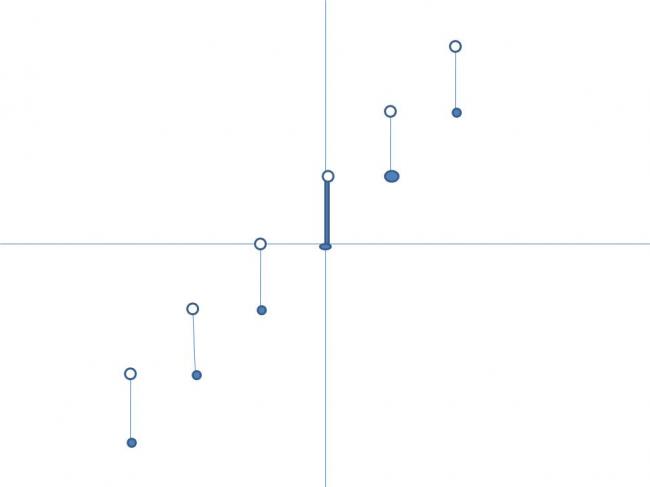
1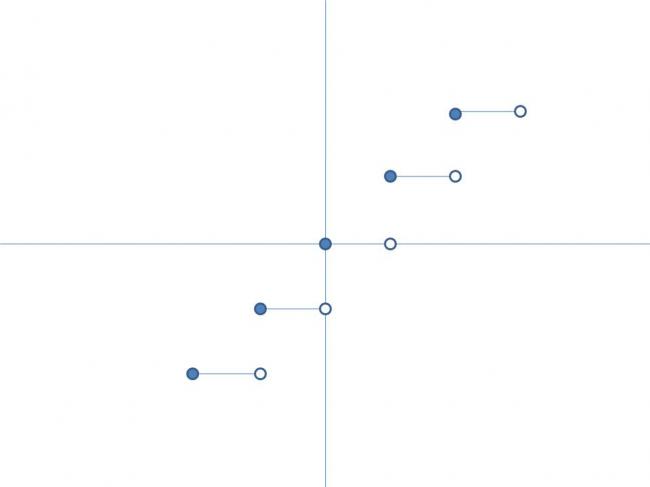 we have the graph of f(x) as
we have the graph of f(x) as
 1
1we can also get the graph of g(x) as this
I'mgiving it in the next post
 we have the graph of f(x) as
we have the graph of f(x) as