i already got wat varun has given
but that will be applicable only iff no of sets is inf
This is very very Interesting question and will make you think! (Hopefully) Even if you dont get the complete solution.. do post the partial ones....
An are sets for all n's (integers!)
The property they follow is that the intersection of any finite of these is non empty.
But the intersection of All of these is empty set.
Give an example of such a set.
There are many ways to achieve this!!!! This might not be a directly relevant question to IIT JEE.. But you will gain insight into sets which is very important for the understanding of functions.
If you are confident of your answer.. use Hide !!! Hide
-
UP 0 DOWN 0 0 32

32 Answers
lol. yes satan u have..
but i am greedyl...
i want to see you guys think more.. so that you could get more independent answers (I mean using some other concepts as well!!)
I will give u the formal proof...
for this one
An={n,n+1,n+2.........}
assume that a number R lies in that set and that set (intersection is non empty)
N=[R]+2
take the intersection of S1, S2........ SN (R will not lie in this set)
hence the intersection is empty.
Hence our assumption that a point lies in the total intersection is wrong!
Hence proved :)
Now that u guys have given a lot of answers.. i will give a slightly different one..
just think if it is correct!!
An = (0,1/n) {The intervalll this is a bit tougher than the ones you guys gave!! The problem is that i studied this sort of .. but i asked you to think about this... }
But you guys did a really commendable job :)
Good work everyone :)
Good one varun.. (u are thinking ;)
How about doing it with intervals now.. ?? (done with enough of sets with single points :)
:P
An ε R - {n}
or Z - {n} ..
I don't think these two will hold good ... (if n ε N)
but this one will
An ε N - {n}
@satan.. it is the proof for finite sets :)
for infinite set N! will be infinity.. !!
skygirl
how is the intersection of all the sets is coming to be null??
there will be a term in each one = "N!"
varun and sky good work...
@celestene well i mean infinite number of sets...
and btw you cant find a solution with finite number of sets :)
a1=multiples of 2
a2=multiples of 3
a3=multiples of 4
a4=multiples of 5
a6=multiples of 6
.
.
.
.
.
aN=multiples of N.
but these will be finite.. right? (n sets!)
how do u make this set infinite?
A small change will help..
ur solution is pretty close to correct!
k i got a general one
consider n diff sets each one containing all but 1 term of given n elements
exluded term for each set is diff
consider that we are inscribing `n` circles in a rectangle such that each circle intersects the remaining `n-2`.
isnt this the same solution (or almost the same as akand?)
or am i mising something?
no no no n is fixed i,e, the number of sets
and instead of being 1,23...n
they can be
k,2k,....nk
you have made a slight mistake satan..
How do u define An in general??
I mena that your definition for An should give A2={1,3} !!!
Just give me An (dont give A1, A2 etc.. that is confusing me!)
A1=1,2,3...n
A2=2,3,4...n+1
...
An-1= n-1,n....
BUT An=1,n+1,...
each set contains n elements
here n can be any integer so we can say there exists infinite possible sets
Yes this is a great example.. i din think of it this way..
good work akand :)
can you give a prooof? ;) (not very difficult)
But I want to see more examples...
how bout the multiples of each number???
like..
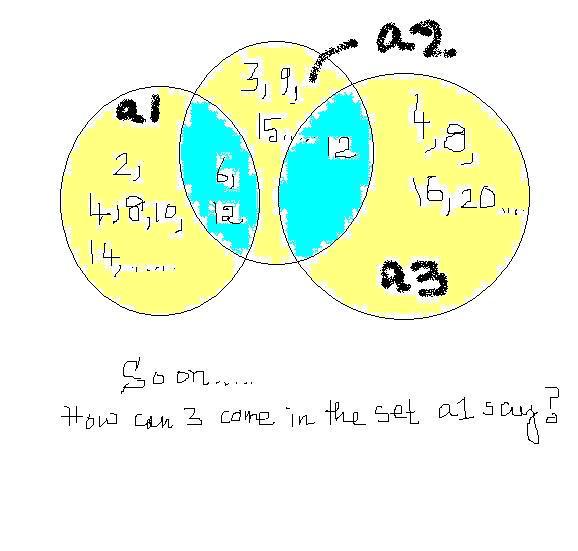
A1={2,4,6,8,10,.....}
A2={3,6,9,12,.....}
A3={4,8,12,...}....etc..
is tht correct nishanth???
..................may be wrong.....
so the intersection of any tow or more sets should be a proper set. whereas the intersection of all the sets must be a null set?
No srinath..
but A1 intersection A3 should be non empty.
THe set you gave are good..
But the question says that the intersection of any finite number of sets is empty set!
b555... dear you cant take a 2n gon.. you have to find infinite such sets. not a constant number of them!!!
I mean you have to give infinite sets
This is not very tough. I guess you did not understand the question :(