9-5-2009 functions

i thought it was a good one. not even worth a look?

This was asked by Kaymant sir long back.
For, any x we have :
f(x+2)=f(x)+2f'(x)+\frac{1}{2}.2^{2}f''(c)
for some c\in (2,x)
This is a corollary of the taylor's theorem.
so, we get :
f'(x)=\frac{1}{2}(f(x+2)-2f''(c)-f(x))
so, we get :
|f'(x)|\leq \frac{1}{2}(|f(x+2)|+2|f''(x)|+|f(x)|)\leq 2

dude , the point is not to obtain the solution.

i am sure not all would have understood your first step. ( EVEN ME)

can u explain your first step?

that was a solution flicked from mathlinks.

http://www.goiit.com/posts/list/differenciation-challenge-no-2-74440.htm has a solution that uses ideas familiar to jee aspirants.

NOTE : above is an extremum case

actually dia is not convex

its a mountain of slopes 1 and -1 and a curve on the top of the mountain to make it differentiable ( as else itll be a inverted V which is not differentiable)

LOGIC :

WLOG lets deal with abv x axis , below x axis wud have same result

for any max f'(x)=c , for occupying min area we need the graph to slope steeply

ie |f"(x)| =1 for major part of the graph

this justifies our choice of taking graph as stated in NOTE .

its evident area is prop to c

now max c implies min area at that c is equal to 2

so proof follows

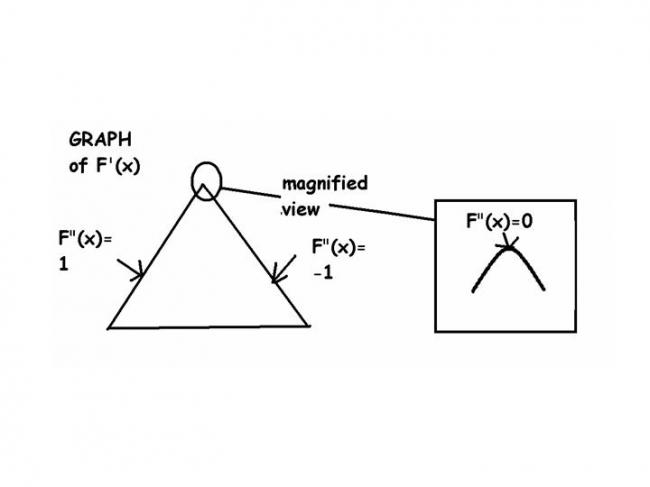
this was the extremum i was saying

its partially concave

ignore first pic