i think the answer is 0
What is the value of
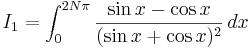
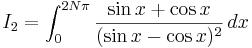
Find I1 - I2 (Given N is any "REALNatural NUMBER" greater than 1!
Well well i thought to give a Real number.. then i thought that it would become a bit too dirty to calculate...
Hint: Give the answer no matter how stupid or tough this question looks. And Pls do check back for the correct answer.. I might have something to say!!! (I dont give easy or "Dirty your hands" question of the days.. Do I?? If the solution is dirty then u might be missing a very simple method to solve it!!)
-
UP 0 DOWN 0 0 12

12 Answers
I1'=0∫2pigiven dx
=(constant) * (-pi/4)∫(7pi/4) (cosx dx/ sin2x)
=0. (Key step= x → x-pi/4)
I2'=0∫2pigiven dx
=(constant) * (pi/4)∫(9pi/4) (cosx dx/ sin2x)
=0. (Key step= x → x+pi/4)
so ans.=0.
i1 =- i2
we get this by subsituting x by 2npi - x
then the equation is reduced to 2i1
we can clearly see that numerator is the differentiation of deno
by subsitution we solve and we get a function of cosec or sec
which will definetly be zero in one time period hence in N time periods also
For I1, take (sin x +cos x) =t and integrate
& for I2, take (sin x -cos x) =t and integrate
I1=I2=sec(2NÎ )-1
hence, I1-I2=0
Yup e=mc^2 and prashant and ith power.. but you are all missing something very small.. (keep thinking.. i am not letting this out that easiliy ;)
I knew that the answer everyone would give is zero!
we can see that the numerator in both i1 and i2 is an periodic function like sinx
dividing it with a +ve periodic function will give a periodic function which will change signs periodically like sinx (sinc we divided it wilth an +ve periodic function)
hence we can say integration of both in n time periods (2pi is the time period of the given functions) will be 0!!
Well thank fully this one is still here..
I cant restore the post o fth others.. but then i hope that You guys get the point i was making..
Ith_power gave the right answer..
I din give a direct reply bocs that would take away your thinking process.. :)
The basic is that the integration that we study at XII th level is the sum of elementary areas... this sum is not defined clearly when function beomes undefined or -infiinity...
so we need to change the definiton for such cases...
let us take sinx+cosx=t
=> (sinx-cosx)dx=-dt
=> -∫dt/t2
=[-1/t]
now simply apply limits... :D
i hope m correct/.... I2 will b done in d same way... hey nishant.. m i correct??
well lord ur method is correct..
but see that 1/t is not defined at zero..
so unless you tell me the limit (or the reason why you are talking about it, I cant be that sure [2] )