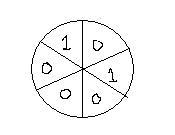
There are 6 slots filled with 1 , 0 in the above order.Now you can operate on any two adjacent sectors and increase the values of both by 1 at a time.you can change the values of two adjacent sectors only at a time.Is it possible that after a sequence of operations al the sectors possess the same value ?
-
UP 0 DOWN 0 0 2

2 Answers
It is a problem of invariance
let a,b be two adjacent elements
after carrying out the operation they become
a+1,b+1
now, there are three sectors in the whole circle .
hence if we consider a and b as a part of one sector .
we get the summation of difference between the two elements of each subset=
a+1-b+1+..=a-b+...=unchanged
if we consider a and b part of different sectors
we get still
x-(a+1)+b+1-y+...=a-b+...=unchanged
when all the elements will be equal then the sum will be =0+0+0=0
but initial sum=1-0+1-0+0-0=2
but it should be invariant
..
hence CONTRADICTION ..
There's a much simpler solution..
the sum of even slots and odd slots be P and Q respectively.
Whenever we add 1 to 2 consecutive slots... P and Q both increase by the same number..
So P-Q remains constnat..
and equal to 2 no matter what.
Hence ... :)