After making exactly (n-1) collisions with the horizontal walls of the board (upper and lower combined) the particle falls into the pocket B.Obviously, the (n-1)th collision takes place on the upper wall.Find out the initial angle θ it should be launched at in terms of d , h , n and e ; e being the coefficient of restitution.
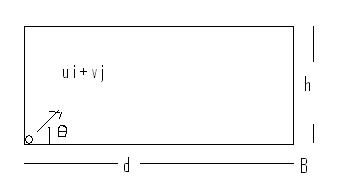
Answer - tan(θ) = (eh/d)((en - 1)/(e-1)) , e ≠1
1we see that the component along the base =u (for all times as impulse from both walls is given perpendiculary always)
after each collision
NEW - (vperpendicular)= e *v(earlier)
finally displacement along y axis = 0
and displacement along x axis = d
=>
h/v + h/ev +h/e2v + .... +h/en-1v = t
and ut=d
furhter solving we get the reqd answer
by substituting v/u=tanθ
1wow......rohan.......u r a child prodigy or wat???? every ques u hav answered in a new method which i hav never even heard of.......... cool man..........
1Well..Rohan ...I appreciate ur work , but be careful of ur Monumental mistakes :)
h/v + h/ev + h/e2v + ...h/e(n-1)v = t
not what you wrote...Careful with signs dude :D
1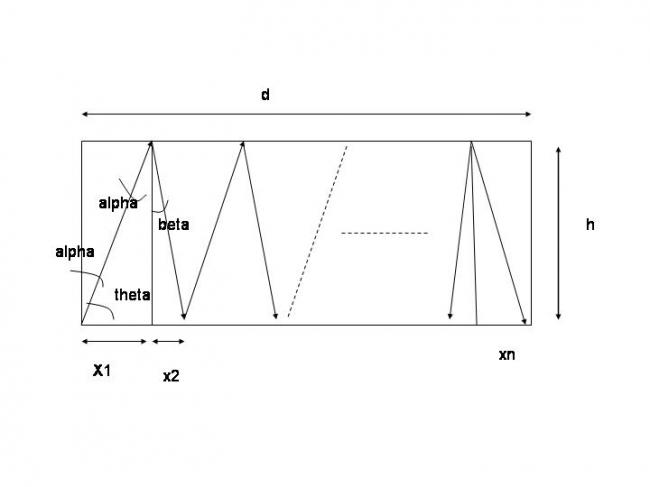
i have got another method ...
x1/h = tanα => x1= h tanα
next tanβ= tanα/e.
x2= htanα/e
x3= htanα/e2
.
.
.
xn = htanα/en-1
now, x1 +x2+ x3+ ... +xn=d
=> h tanα [1+ 1/e + 1/e2 +..... +1/en-1 ] =d
=> h tanα [(1/e)n-1 / (1/e)-1] = d
=> tanα = d/ h [(1/e)n-1 / (1/e)-1]
=> α = tan-1 { d/ h [(1/e)n-1 / (1/e)-1]}
so θ = 90 - α.
1good work..but too tedious...try to use subtle elegant ways that saves time :)