I THINK IT IS IN
H.C VERMA
HEAT TRANSFER
Q.no. 37
Two bodies of masses m1 and m2 and specific heat capacities s1 and s2 are connected by a rod of lenght L crossectional area A,thermal conductivty K and negligible heat capacity.The whole system is thermally insulated.At time t=0 the temperature of the first body is T1 and the temperature of second body is T2(T2>T1).Find the temp. difference betw. 2 bodies at time t.
plz help me with this Q.
thanku.
-
UP 0 DOWN 0 0 19

19 Answers
Let at some later time t, the temperatures of the two bodies be T1'(t) and T2'(t) respectively. So that the temperature difference is ΔT(t) = T1'(t) &ndash T2'(t) as a function of time. The heat current at this instant is given by
\dot{q}=kA\dfrac{\Delta T}{L} ------ (*)
In the next infinitesimal interval of time δt, the heat current transfers \dot{q}\ \mathrm \delta t from first body to the second one. So the first body looses this amount of energy because of which its temperature drops to T1'(t+δt) while the second body gains this much of energy so its temperature increases to T2'(t+δt). So the new temperature difference is
ΔT(t+δt) = T1'(t+δt) &ndash T2'(t+δt)
So we have
ΔT(t+δt) &ndash ΔT(t) = (T1'(t+δt) &ndash T1'(t)) &ndash ( T2'(t+δt) &ndash T2'(t)) ------- (1)
But \dot{q}\ \mathrm \delta t = &ndash m1 s1 (T1'(t+δt) &ndash T1'(t)) = m2 s2( T2'(t+δt) &ndash T2'(t))
Hence, (1) becomes
ΔT(t+δt) &ndash ΔT(t) = &ndash \dot{q}\ \mathrm \delta tm1s1 &ndash \dot{q}\ \mathrm \delta tm2 s2
from where we obtain
&ndash ΔT(t+δt) &ndash ΔT(t)δt =\dot{q}\left(\dfrac{1}{m_1s_1}+\dfrac{1}{m_2s_2}\right)
In the limit δt →0, we get
\dot q = -\dfrac{1}{C}\dfrac{\mathrm d(\Delta T)}{\mathrm dt}
where
C=\dfrac{1}{m_1s_2}+\dfrac{1}{m_2s_2}
Substituting this in (*), we get
-\dfrac{1}{C}\dfrac{\mathrm d(\Delta T)}{\mathrm dt}=kA\dfrac{\Delta T}{L}
which could be integrated to give
\boxed{\Delta T =(T_1-T_2)e^{-t/\tau}}
where
\dfrac{1}{\tau}=\dfrac{kA}{L}\left(\dfrac{1}{m_1s_1}+\dfrac{1}{m_2s_2}\right)
now
dT_{1}=\frac{KA\Delta T}{m_{1}s_{1}L} dt
similarly
dT_{2}=\frac{KA\Delta T}{m_{2}s_{2}L} dt
dT=\frac{KA\Delta T}{m_{1}s_{1}L} dt+\frac{KA\Delta T}{m_{2}s_{2}L} dt
now solve this by integrating it (here \Delta T is variable )
(i think there is a Sign convention error )
let at time t the temperature difference is \Delta T
now heat transfer in very small time is
dQ=\frac{KA\Delta T}{L}d t
now heat losed by one part is = heat gained by other part
dQ=m_{1}s_{1}dT_{1}=m_{2}s_{2}dT_{2}
where dT(1) and dT(2) are small change in temp of m(1) and m(2)
now the total small temperature difference is dT=dT_{1}+dT_{2}
i will complete the soln in next post
yar just use haet current principle that heat passis through the both bodies are sme( heat current=κA TEMP DIFF/d) let the temp of junction any
ya i got till der
but jus unable to do teh integrating part.....i mean ans isnt matching
we shud do lik this na
dT/dt=the exp which u got in teh last step
got to go ........ i'll post rest of solutions later........[2][2][2][2][2][2]
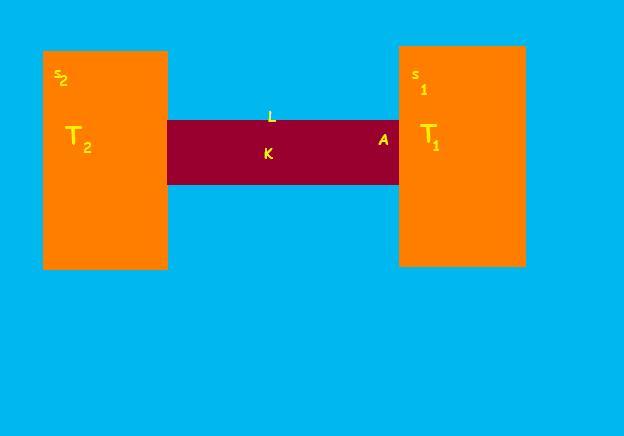
lets analyze
heat flowing ΔQ is proportional to ΔT, A , Δt and inversly proportional to L
so, \Delta Q=K\frac{A\Delta t\Delta T}{L}
so,\frac{\Delta Q}{\Delta t}=K\frac{A\Delta T}{L}
or reducing Δt to infiniitesimally small time we get,
\frac{dQ}{dt}=K\frac{A\Delta T}{L}
this can be found in any book.....
but then is the twist...
the temp difference ΔT changes with time...
initially, in dt time heat leaving second body is K\frac{A(T_{2}-T_{1})}{L}
so temp fall in second body is K\frac{A(T_{2}-T_{1})}{m_{2}s_{2}L}
rise intemp in other body is K\frac{A(T_{2}-T_{1})}{m_{1}s_{1}L}
so for next dt period, ΔT is T_{2}-T_{1}-K\frac{A(T_{2}-T_{1})}{m_{1}s_{1}L}-K\frac{A(T_{2}-T_{1})}{m_{2}s_{2}L}
can u plz poast a complete soln....
seriously i m not able to get it [2]
plz help
find the amount of heat transferred from body2 to body1
since t2>t1 and then find the two new temps at time t