That's not correct. It is not an isothermal process.
A straight glass tube with its lower end sealed has a length \ell=152\ \mathrm{cm}. The lower half contains one mole of an ideal diatomic gas. The top half contains mercury and the top of the tube is open to atmosphere (atmospheric pressure p_0=760\ \textrm{mm of Hg}). The gas is now heated slowly. How much heat is needed to be transferred to the gas to push out all the mercury? Take the cross section of the tube to be 1 cm2.
-
UP 0 DOWN 0 7 14

14 Answers
See
For the gas
P1V1 = P2V2
760*22400= P2 * 76
P2 = 224000mm of Hg pressure
Now 760mm of Hg is 1.0135 *105
224000 ?
295*1.0135*105
W = PΔV
ΔV = 76
1m3 = 1m*1m*1m
1m3 = 106cm3
? 76
76*10-6
W = 295 * 1.0135*10 5 * 76 *10-6
W = 295 * 7.6 *1.0135
W = 2272J
sorry for the late rply there was again a power ctoff
heres the soln (you can say the steps)
initially length of the mercury column= l/2
let at a time t it be l/2-x
then pressure = P0+Ïg(l/2-x)
volume = (l/2+x)A
initial pressure
P0+pg(l/2)
volume=(l/2)A
equating we get
temperature as a function of x (as the initial temp can be found out as all initial data is given)
sry due to lack of time i am making it short
dQ=dU+dW
dQ=nCvdT + (P0+Ïg(l/2-x))Adx
we know T as fn of x
thus we get dT as g(x)dx
integrate from x=0 to l/2
we get answer
That's not correct satan92...
May be it will helpful, if you plot the variation of the molar heat capacity of the gas as the function of its volume.
let us take a particular time when x cm of mercury is abv the thing
therefore pressure ==>
Patm + rho gx ..............
now V = A(l/2-x+l/2)
integral PdV = NET WORK.............
P(ini)V(ini)/nR = T(INI) [P(INI) =Patm + ro g l/2 V(INI) = A l/2 ]
P(final)V(FINAL)/nR = T(final) [P(FINAL) = Patm V(FINAL) = Al ]
therefore
U = nCv(T(FINL) - T(INI.))
Q = U + W ....................
thus we can get Q ............................
i am really sorry if i lacked respect ..
actually i was not able to figure out the flaw in any way .. but now i have figured out ... (due to sir's help)
@iitimcomin , u need to convert everything in terms of dx so that you can find the molar heat capacity of the process ... believe me if you get the expression , you will realize something important :)
Okay here is the solution. First, note that
\dfrac{\ell}{2}=76\ \textrm{cm} which correspond to atmospheric pressure p_0.
Let V_0=\dfrac{A\ell}{2}, so that the initial and final volume of the gas are, respectively, V_0 and 2V_0.
Also, note that the initial and final temperatures of the gas are equal.
When x length of mercury has been pushed out, the gas volume V=A\left(\dfrac{\ell}{2}+x\right)=V_0\left(1+\dfrac{2x}{\ell}\right)\qquad (1)
and the pressure
p=p_0+p_0\left(\dfrac{\frac{\ell}{2}-x}{\frac{\ell}{2}}\right)=p_0\left(2-\dfrac{2x}{\ell}\right)
From (1), we see that,
\dfrac{2x}{\ell}=\dfrac{V}{V_0}-1
so that the gas pressure
p=p_0\left(3-\dfrac{V}{V_0}\right) (2)
This is the process in the p-V coordinates and the graph is as follows:
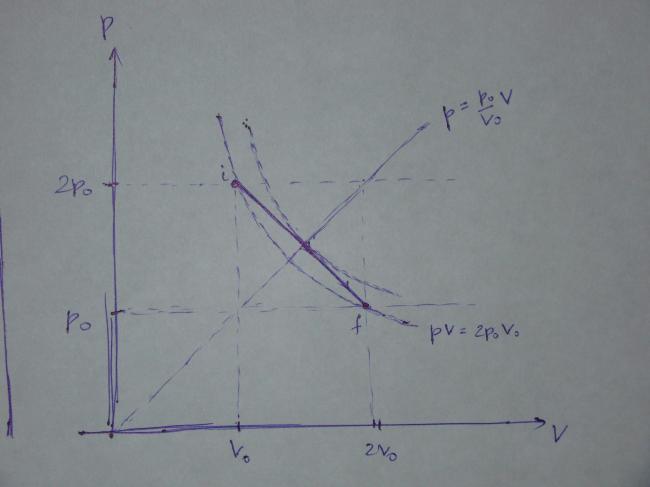
Note that the points i and f lie on the same isotherm whose equation is
pV=2p_0V_0.
It is quite obvious that the gas temperature attains the maximum value where the line
\dfrac{p}{p_0}=\dfrac{V}{V_0} meets the process given by (2), i.e. at the intersection of
\dfrac{p}{p_0}=\dfrac{V}{V_0} and p=p_0\left(3-\dfrac{V}{V_0}\right)
which gives
\dfrac{V}{V_0}=\dfrac{3}{2} at maximum temperature. Alternatively, using pV=nRT, we get
T=\dfrac{pV}{nR}=\dfrac{p_0V_0}{nR}\cdot \dfrac{V}{V_0}\left(3-\dfrac{V}{V_0}\right)\qquad \quad (3)
from where it is easily seen that the temperature T attains the maximum at \dfrac{V}{V_0}=\dfrac{3}{2}.
Let's determine the molar heat capacity of the gas for the process:
C=\dfrac{\delta Q}{n\,\mathrm{d}T}= C_v+\dfrac{p\,\mathrm{d}V}{n\,\mathrm{d}T} = C_v + \dfrac{p_0}{n}\left(3-\dfrac{V}{V_0}\right)\dfrac{\mathrm{d}V}{\mathrm{d}T}
From (3) we get
\dfrac{p_0}{n}\dfrac{\mathrm{d}V}{\mathrm{d}T}=\dfrac{R}{3-2\frac{V}{V_0}}
Accordingly, we get
C=C_v + \dfrac{3-\frac{V}{V_0}}{3-2\frac{V}{V_0}}\,R
Using the fact that for diatomic gas Cv=5R/2, we get ultimately, after slight simplification,
\boxed{C=\dfrac{3R}{2} \left(\dfrac{7-4\frac{V}{V_0}}{3-2\frac{V}{V_0}}\right)} (4)
The following graph shows that plot of C vs the ratio V/V0 till all the mercury has been pushed out.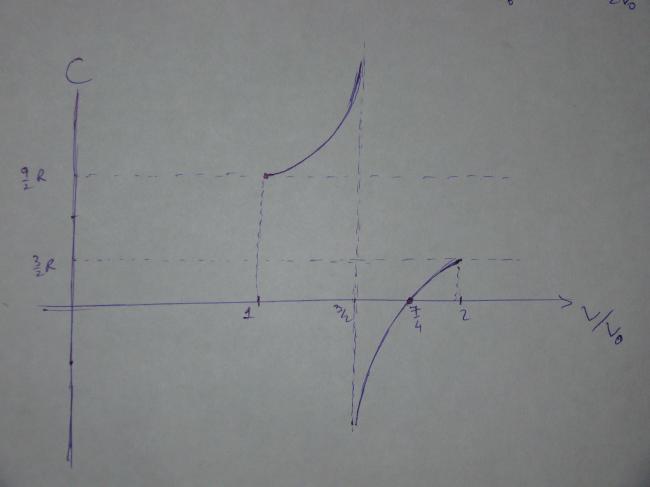
The graph shows some interesting behavior. The curve is singular (the molar heat capacity approaches infinity) at \dfrac{V}{V_0}=\dfrac{3}{2} because at this point the pV plot of the process is a good approximation to the isothermal corresponding to the maximum temperature. During an isothermal process, heat is transferred but the temperature does not change, and this is why the molar heat capacity tends to infinity. Beyond this point, the molar heat capacity becomes negative, which means that in spite of the positive heat transfer, the internal energy of the gas decreases because the work done by it in expanding is greater than the heat transferred.
The most interesting part of the curve occurs when \dfrac{V}{V_0}=\dfrac{7}{4}, i.e. when only a quarter of the mercury is left in the tube. At this point the molar heat capacity becomes zero and implies that the process is adiabatic, since there is a change in temperature without any heat transfer. At this point, the straight line describing the process is tangent to an adiabatic curve. Beyond this point, the temperature decreases further but the molar heat capacity becomes positive; this can only correspond to the system being cooled.
If more heat is given to the system, the representative point no longer follows the straight line but continues along the adiabatic one. The temperature of the gas does decrease, but not by as much as the straight line would suggest. The decrease in the internal energy is equal to the work done against atmosphere (while lifting the mercury) and in accelerating the ejected mercury.
Thus, we see that in order to push out all the mercury, it is necessary to transfer heat only till \dfrac{V}{V_0}=\dfrac{7}{4} starting from \dfrac{V}{V_0}=1.
Thus, the heat transferred
Q=\int nC\ \mathrm{d}T = \int_{V_0}^{7V_0/4}C\ \dfrac{p_0}{R}\left(3-\dfrac{2V_0}{V}\right) \mathrm{d}V
Plugging in the expression for C and a bit of simplification give us
Q=\dfrac{3}{2}p_0 \int_{V_0}^{7V_0/4}\left(7-\dfrac{4V_0}{V}\right) \mathrm{d}V
from where we finally obtain the heat transferred as
\boxed{Q=\dfrac{27}{16}p_0 V_0}
brilliant ............ its an honour to learn frm u sir ..............