THERMAL PHYSICS-Solve these!!!@@@

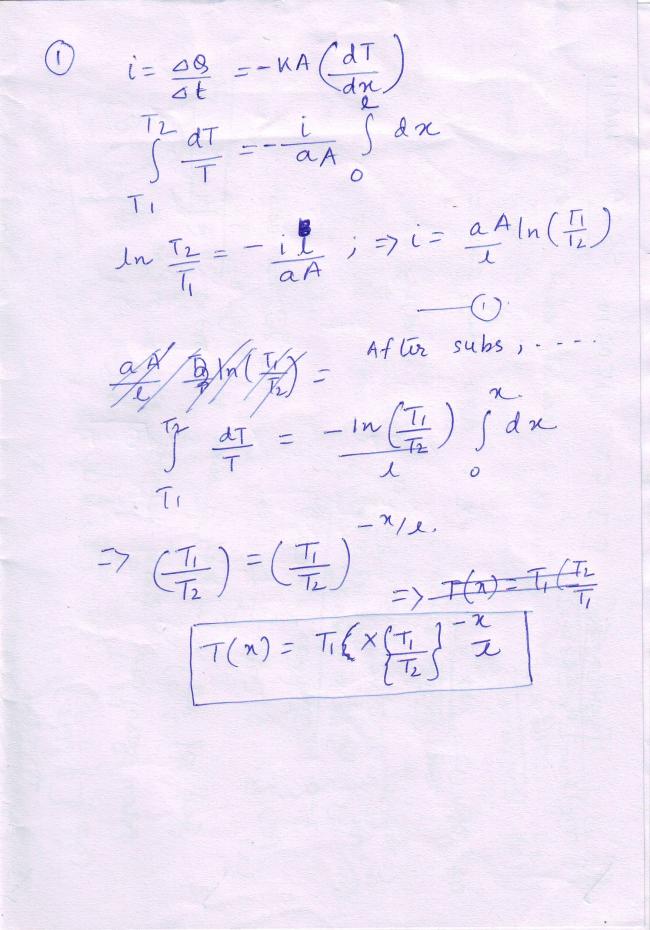
1) A rod of length l with thermally insulated lateral surface consists of material whose heat conductivity
Coefficient varies with temperature as k=α/T, where a is a constant. The ends of the rod are kept at
Temperatures T1 and T2. Find the function T(x), where x is the distance from the end whose temperature is T1, and the heat flow density.

2) a) Thermalconductivity in a wall varies as K = K0T2. Find the value of temperature at whi ch mean
Thermal conductivity be evaluated so that same heat flows through the wall. T1 and T2 are the
Temperature of the ends?

3) A hollow sphere of mass m is made of a material having specific heat capacity s J/kg-K. Inner and
Outer surfaces of the sphere have area am2 and A m2 respectively. Sphere is suspended by a light
non –conducting thread from ceiling of a room. Assuming sphere material to be highly conducting
and its emissivity e, calculate time taken by the sphere to cool from T10C to T20C when room
temperature is T00C. (Take Stefan’s constant = σ Wm-2K-4).

4) The shell of a space station is a blackened sphere in which temperature T = 500 K is maintained due
To the operation of appliances of the station. Find the temperature of the shell if the station is
Enveloped by a thin sperical black screen of nearly the same radius as the radius of the shell. The
Conduction of heat between the shell and the screen is negligible.