1r u sure about ur ans????
bcoz this is one of the ques which i was given imy coaching..in trigo test..i also marked a option...but the ans is "c" and
it may be possible that c is not correct...
Consider the set of points (x,y) in the plane which satisfied x2+y2<=100 and sin(x+y)>=0. solve the following ques.
1.) the region given by sin(x+y)>=o will be
a) angular region between two concentric circles
b) all points in the plane except the ones lying within y+sinx
c) union of region between parallel lines
d) union of region between two concentric circles
2.) let A1 and A2 be the area of regions within x2+y2<=100 which satisfy sin(x+y)>0 and sin(x+y)<0 then
a) A1>A2
b) A1<A2
c) A1=A2
d) none of these
-
UP 0 DOWN 0 0 14
14 Answers
62Hint to Part 1)
sin x+y +ve means
0<x+y <pi
so it is like 2 parallel lines..
thtere will be many of them..
62Part 2 is a tricky question!
I will give another hint..
think symmetry! (how is for u to think!)
1ya even i thought the same for part 1
but in part 2 will there be two semi circles inside...the circle formed by the first eqaution???? ( A1=A2
62no it wont be semicircles..
it will be patches of lines.. like the zebra crossing!)
think again!
1hey, i got the solution of (2)
if A1 represents arera between sin(x+y)≥0
& x2+y2≤100
& is A2 represent area b/w sin(x+y)<0 &
x2+y2≤100
then A1>A2
please, ny one tell me how to insert figure so that i can post the solution
62when u reply there is an upload image button click it ... u can upload images :)
162C is the right answer
A1=A2 dont worry rupal.. i just wanted to see his soln..
do u want me to ost the soln?
62
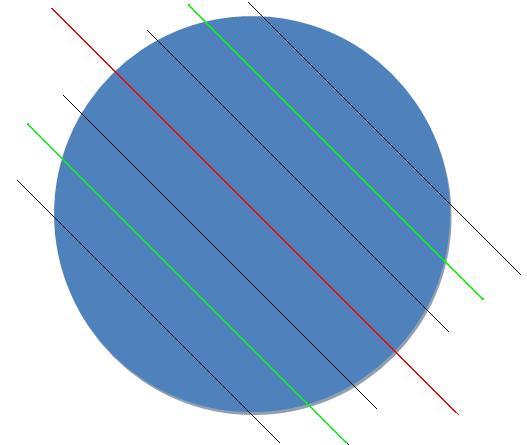
I know this is a very bogus image :P
but yeah lets see this..
the middle red line is x+y=0
the first black lines are x+y=±Î
the second green lines are x+y=±2Î
the third black lines are x+y=±3Î
Now the place between the red and black line on the top is for sin(x+y)>0
correspondingly between red and black below is sin(x+y)<0
there is this symmetry.
the larger circle is of radius 10
I hope this helps :)
1
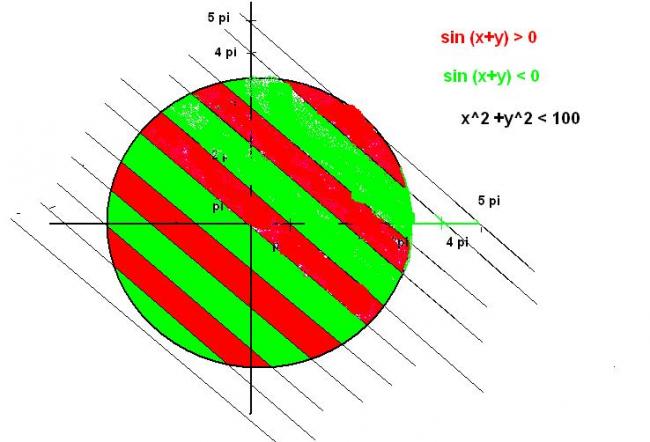now, here's my solution
given x2+y2≤100
now, by use of foll. inequility
2(x2+y2)≥(x+y)2
we get,
-10√2≤(x+y)≤10√2..............(i)
for sin(x+y) > 0
we get,
2nΠ≤(x+y)≤(2n-1)Π...........(i) (n is ny integer)
solving (i) & (ii)
2nΠ≤10√2 & (2n+1)Π≥-10√2
-2.75≤n≤2.25 so, n = 2,1,0,-1,-2
for sin(x+y)<0
(2m-1)Π≤(x+y)≤2mΠ........(iii) (m is ny integer)
solving (i) & (iii)
we get, -2.25≤m≤2.75 so, m = -2,-1,0,1,2
plotting the functions in graph we have,
the green portion for sin(x+y)<0
red portion for sin(x+y)>0
clearly
A1 = A2 ( for x,y belongs to R)
A1 > A2 ( for x,y belongs to R+)
& A1 < A2 ( for x,y belongs to R-)
HOPE I AM CORRECT.........
1SORRY, THERE WAS A TYPING mistake
IN MY PREVIOUS TO PREVIOUS POST.....
AS I HAVE STATED IN MY PREVIOUS POST
A1 = A2 (for x,y belongs to R)
so ans is (c)..........
SORRY, I TOOK TIME IN TYPING......
62yes u have done a good job.. and a very wonder ful way of writing the answer...
far better than i did :)