If ABCD is cyclic quadrilateral, show that AC . BD = AB . CD + BC . AD
1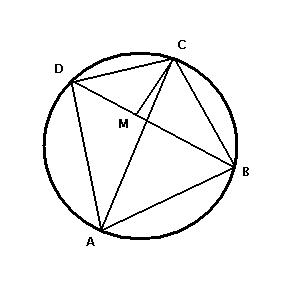
On the diagonal BD locate a point M such that angles ACB and MCD be equal. Since angles BAC and BDC subtend the same arc, they are equal. Therefore, triangles ABC and DMC are similar. Thus we get CD/MD = AC/AB, or AB·CD = AC·MD.
Now, angles BCM and ACD are also equal; so triangles BCM and ACD are similar which leads to BC/BM = AC/AD, or BC·AD = AC·BM. Summing up the two identities we obtain
AB·CD + BC·AD = AC·MD + AC·BM = AC·BD
1Btw..this is known as Ptolemy's Theorem.
http://en.wikipedia.org/wiki/Ptolemy%27s_Theorem
21Let AB = a, BC = b, CD = c, DA = d
using cosine rule in ΔABC and ΔADC, we get :
AC2 = a2 + b2 – 2ab cos B
AC2 = c2 + d2 – 2cd cos D
and B + D = π
⇒ cos B + cos D = 0
⇒ AC2 (cd + ab) = (a2 + b2) cd + (c2+ d2) ab
⇒ AC2 = (a2cd+ c2ab) (b2cd +d2ab)cd+ ab
Similarly by taking another diagonal BD, we can show that :
BD2=(ba+ cd)(bd+ ca)da +bc
Multiplying the two equations
⇒ (AD . BD)2 = (ac + bd)2
⇒ AC . BD = ac + bd
⇒ AC . BD = AB . CD + BC . AD