area = 12 + 7√3 ?
Given an isosceles triangle whose one angle is 120 degree and radius of its incircle is √3. Then the area of the triangle in square units is:
-
UP 0 DOWN 0 0 6

6 Answers
Asish Mahapatra
·2009-03-27 03:52:30
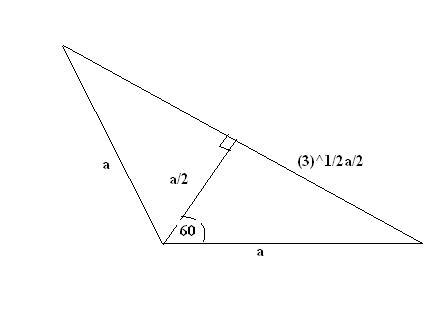
s = (2a+√3a)/2
area = 1/2*a/2*√3a = √3a2/4
So, r= area/s = √3a2/4/(2a+√3a)/2 = √3
Solving we get a=2+√3
so area = √3a2/4 = 12+7√3