66Or simply consider f:[0,\pi/2]\longrightarrow \mathbb{R} defined by
f(t)=t-\sin t
For t\in(0,\pi/2),
f^\prime(t)=1-\cos t>0
Hence, f is strictly increasing. As such for
0<x<y<\pi/2
f(x)<f(y)\quad\Rightarrow \ x-\sin x<y-\sin y
5 Answers
24x<y ----------(1)
=> sinx <siny -------(2)
now in (0,pi/2)
both x-sinx and y-siny are increaisng functions
=> x-sinx<y-siny
1As x<y,
sinx<siny, sinx is increasing in (0,∩/2)
From the graph,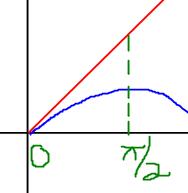
x>sinx
or,x-sinx>0
=>∂(x-sinx)/∂x=1-cosx >0 for x in (0,∩/2)
Therefore x-sinx is increasing funtion
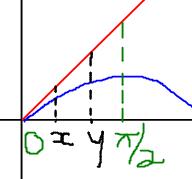
So, as x<y
x-sinx<y-siny
[339]
66
341Just for the heck of it one more solution, this one without calculus.
Since x,y \in \left[0, \frac{\pi}{2} \right], we have \frac{y-x}{2}, \frac{y+x}{2} \in \left[0, \frac{\pi}{2} \right]
Now \sin y - \sin x = 2 \sin \frac{y-x}{2} \cos \frac{y+x}{2} < 2 \ \left(\frac{y-x}{2} \right) \cos \frac{y+x}{2} < y-x
Hence x - sin x < y - sin y