11I am getting √3 and -1/√3 as the answer..:)
Q . Solve:
cos-1 x2-1x2+1 + tan-1 2xx2-1 = 2Ï€3
I'm getting ±√3 but the book says √3, 2 - √3! [7]
-
UP 0 DOWN 0 0 12
12 Answers
30My working was similar to yours except that I took,
2cos-1 x2-1x2+1 = 2Ï€3
x2-1x2+1 = 12
Giving, x= ±√3
262you are making mistake guys.!!!
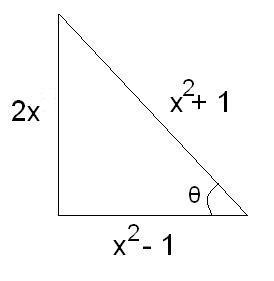
cos-1 1-x21+x2 = tan-12x1-x2
but in the question it is cos-1x2-11+x2.
262just replace x=tanθ2. then cos-1x2-1x2+1 = cos-1 sin2θ/2 - cos2θ/21 = cos-1 (-cosθ) = π -θ
while tan-1 2x1-x2 = θ
1here x2 should be<1
so x2-1<0
tan-12xx2-1<0
then i am confused what to do after this
aisa solve hoga kya?
30@Aditya - All said and done, but how are we getting the given answer? I might be missing something so please if you can explain. :)
@Nishant sir- Please tell us where we are going wrong!
262the answer in the book must be surely wrong. bcoz if u proceed with my method as i have given before, we get π -2θ = π/3 (where θ=2tan-1x )
therefore x= 1/√3 , √3
1the book ans may be correct........
i got 2-√3
let x= tanθ
cos-1 (-cos 2θ) + tan-1(-tan 2θ) = 2pi/3
pi -2θ-2θ = 2pi/3
θ=pi/12
tan pi/12 = 2 - √3