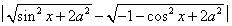is,whee a and x are reals
1708\hspace{-16}\mathbf{M=\mid \sqrt{\sin^2 x+2a^2}-\sqrt{-1-cos^2 x+2a^2}\mid}$\\\\ So for the expression $\mathbf{M}$ is Max.\;,\\\\ value of $\mathbf{\sqrt{-1-cos^2 x+2a^2}}$ is Min.\\\\ So Min. value of $\mathbf{\sqrt{-1-\cos^2 x+2a^2} = 0}$\\\\ So $\mathbf{-1-\cos^2 x+2a^2=0\Leftrightarrow 2a^2-1=\cos^2 x}$\\\\ $\mathbf{2a^2-1=1-\sin^2 x\Leftrightarrow 2a^2+\sin^2 x=2}$\\\\ So $\mathbf{\sqrt{2a^2+\sin^2 x}=\sqrt{2}}$\\\\ So Max. value of $\mathbf{M=\sqrt{2}}$
