2305
(ca+cb)2=(cosec(θ)+sec(θ))2=(cosec(θ)+cosec(90-θ))2
cosec(θ)+cosec(90-θ)≥2cosec(90+θ-θ2)=2cosec(45)=2√2
(ca+cb)2≥8
Answer -8.
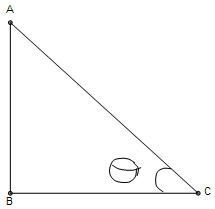
Given that a,b,c are the sides of ΔABC which is rt.angled at C.Then the min. value of (c/a + c/b)2 is ??
-
UP 0 DOWN 0 0 4
4 Answers
2305
1708To Shaswata Roy
Have you any idea about Holder Inequality.
How Can we apply Holder Inequality in Calculating Min. value of
\hspace{-16}\bf{\left(a.\sec \theta+b.\tan \theta \right)}. where a,b>0
Thanks
2305If I am not wrong Holder's inequality sates that,
\inline \dpi{200} \sum_{i=1}^{n}a_{i}b_{i}\leq (\sum_{i=1}^{n}a_{i}^{p})^{\frac{1}{p}}(\sum_{i=1}^{n}b_{i}^{q})^{\frac{1}{q}}
for1p+1q=1
For p=q=2,we get the Cauchy-Schwarz inequality i.e,
\inline \dpi{200} asec(\theta)+btan(\theta)\leq (\sqrt{a^{2}+b^{2}})\sqrt{(sec^{2}(\theta)+tan^{2}(\theta))}
Minimum will be obtained when a/b = secθ/tanθ = cosecθ
