kardo yaar koi..
In triangle ABC , AD is the altitude from A on BC , if angle B =45 degrees and c>b and AD = abc/(2(c^2-b^2)) , then angle A =
1. 30
2 .45
3 .60
4 .75
-
UP 0 DOWN 0 0 5

5 Answers
well if u draw the figure, u can straight away rule out a and b. now after some solving, we get \frac{a}{\sqrt{2}b}=\sin A
which would be satisfies by 60 degrees.
hence answer c
i ruled out a and b. got the relation described above, then straightly put A=60 degrees. got the above relation when i started from back. hence the answer
this is more like elimination..
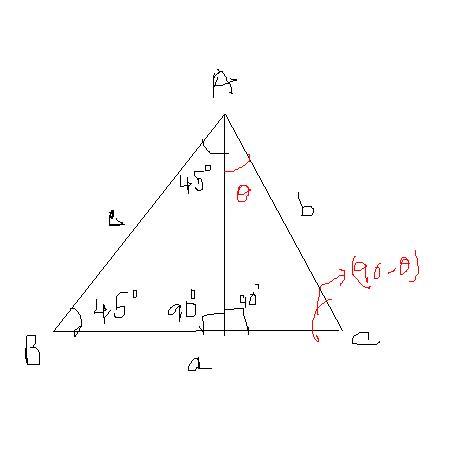
isme..
condition given is c>b...
now, b will br equal to c if C=45°.
and b>c for C< 45° . [jus draw]
so, C has to be >45°
=> 90-θ > 45 => θ<45
options a and b are stupid.. because...
A will anyhow be >45.
now do some back calculation... u get the ans....