Number os solutions of the eqn tan x+ sec x= 2cos x ,
lying in the interval [0,2∩) is
a) 0
b)1
c)2
d)3
23tanx+secx= 2cosx
multiply by cosx
sinx+ 1 = 2cos2x
sinx+1 = 2- 2sin2x
2sin2x+ sinx - 1 = 0
2sin2x + 2sinx - sinx - 1 = 0
2sinx(sinx+1) - (sinx+1) = 0
(sinx+1)(2sinx-1) = 0
sinx= -1 , sinx = 1/2
so x = 3pie/2 , or x = pie/6 ,or x =pie - pie/6
but for x = 3pie/2 , tanx isnt defined
hence x = pie/6 or 5pie/6
hence 2 solutions
is the ans correct ?
y m i not able to open latex ?
62Good work
btw for the number of solutions, you could also have looked at
sinx+ 1 = 2cos2x
sin x = cos (2x)
and from graph tried to conclude the same!
23yes sir , i do want to improve my graphing abilities , and m learning the same from Tiit !!! and some frndz wich i made here !!! [1]
1ok....i hav to say something [3]
will teh no of point of intersection of grphs sin x and cos (2x) give the no of solns of tan x+ sec x= 2cos x
bec no of point of intersection of grphs sin x and cos (2x) will be 3......3pi/2 will also be its soln
but for this tan x+ sec x= 2cos x 3pi/2 is not a soln.....bec tan(3pi/2) is not defined
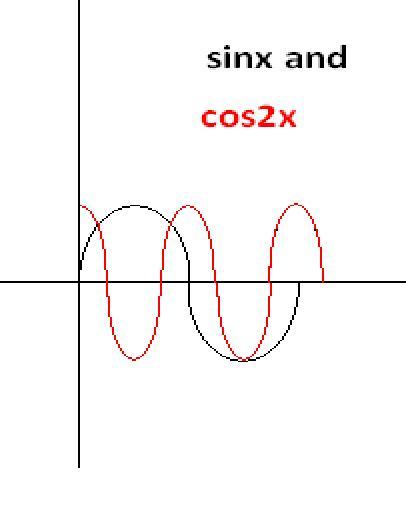
1u r rong i guess qwerty
sin 270=-1
cos(2*270)=-1
so how can u say 3pi/2 is not a soln of sinx=cos2x
341Another way:
\tan x + \sec x = 2 \cos x \Rightarrow \sec x - \tan x = \frac{1}{2 \cos x} = \frac{\sec x}{2}
\Rightarrow \sec x = 2 \tan x
From the 1st eqn this implies
\cos x = \pm \frac{\sqrt 3}{2} and cos and tan must both have the same sign.
So 2 solutions
