am close 2 da ans...
can ne1 tell how 2 deal wid a2 + b2 + c2???
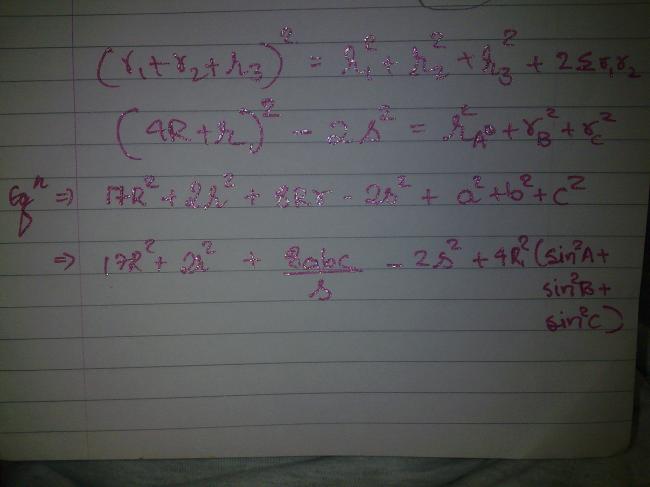
aage help chahiye!!!!!!!!!!
a2 + b2 + c2 + r2 + rA2 + rB2 + rC2 + R2 = ...........
(A) 7 R2 (B) 7 r2
(C) 17 R2 (D) 17 r2
a,b,c : sides of ∆le ABC
r : inradius rA,rB,rC : exradii
R : circumradius
am close 2 da ans...
can ne1 tell how 2 deal wid a2 + b2 + c2???
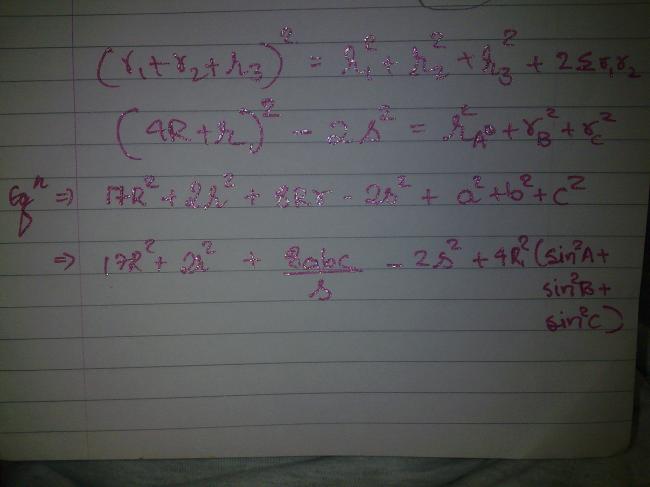
aage help chahiye!!!!!!!!!!
AAGE KYA KARE????
SUBHASH'S IDEA IS COOL N CHIKY....
BUT THER MUST B A MORE GENERAL WAY TO IT.... HELP.....
Its verry long................I would be using some things as such(the bold ones)........if u want i will explain later.....
(r1+r2+r3-r)2=r12+r22+r32+r2-2r(r1+r2+r3)+2(r1r2+r2r3+r3r1)
We know that r1+r2+r3-r=4R
and r1r2+r2r3+r3r1=s2
=> (4R)2=r12+r22+r32+r2-2r(r1+r2+r3)+2s2
=>r12+r22+r32+r2=16R2+2(rr1+rr2+rr3)-2s2 ----------------(1)
Also, 2(rr1+rr2+rr3)=2[S2/s(s-a) +S2/s(s-b)
+S2/s(s-c)]
=>2S2 [(s-b)(s-c)+(s-c)(s-a)+(s-a)(s-b)]
=>2[3s2-s(b+c+c+a+a+b)+bc+ca+ab]
=>2[3s2-s.4s+bc+ca+ab]
=> -2s2+2(ab+bc+ca)
From(1)
r12+r22+r32+r2=16R2-2s2+2(ab+bc+ca)-2s2
=>16R2-[(a+b+c)2-2(ab+bc+ca)]
=>16R2-(a2+b2+c2]
=>r12+r22+r32+r2+a2+b2+c2+R2=17R2
I am out of breath now...................Some typo may be there.........plzzzzz have some pity on me..........
cooooooooooooooooooooooooooooooooooooooooooooool EUREKA
GR8 EFORT 4 SUCH A MARATHN....................................................
Another method.....
(r2+r12)+(r22+r32)
= 16R2sin2(A/2) [ sin2(B/2) . sin2(C/2) + cos2(B/2) . cos2(C/2) ]
+
16R2cos2(A/2) [ sin2(B/2) . cos2(C/2) + cos2(B/2) . sin2(C/2) ]
= 16R2sin2(A/2) [ {(1- cos B)/2} . {(1- cos c)/2} +
{(1+ cos B)/2} . {(1+ cos C)/2} ]
+
16R2cos2(A/2) [ {(1- cos B)/2} . {(1+ cos c)/2} +
{(1+ cos B)/2} . {(1- cos C)/2} ]
= 4R2sin2(A/2) [ 2 + 2 cos B . cos C ]
+
4R2cos2(A/2) [ 2 - 2 cos B . cos C ]
= 8R2 + 4R2 [ {cos (B+C) + cos (B-C)} . {sin2(A/2) - cos2(A/2)} ]
= 8R2 - 4R2 [ {cos A . (- cos A)} + {cos (B+C) . cos (B-C)} ]
= 8R2 + 4R2 [ cos2A + cos2B - sin2C ]
= 8R2 + 4R2 [ 2 - (sin2A + sin2B + sin2C) ]
= 16R2 - (a2 + b2 + c2)
So,
(a2 + b2 + c2 + r2 + r12 + r22 + r32) + R2 = 16R2 + R2 = 17R2