Properties of Triangles

DUE TO OBVIOUS REASONS, I WILL NOT BE ABLE TO GIVE U ALL THE THREE VARIANTS OF A FORMULA (IF THEY ARE PRESENT)

THE BEST WAY TO LEARN THESE FORMULAS IS TO NOICE THE PATTERN IN EACH OF 'EM AND REMEMBER THAT PATTERN

1) Sine Rule:

\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}

2) Cosine Rule:

cosA=\frac{b^2+c^2-a^2}{2bc}

3) Projection Formulae:

a=b cosC+c cosB

4) Napier's Analogy:

tan\left(\frac{B-C}{2} \right)=\frac{b-c}{b+c}cot\frac{A}{2}

5) Half Angle Formulae:

sin\frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{bc}}

cos\frac{A}{2}=\sqrt{\frac{s(s-a)}{bc}}

tan\frac{A}{2}=\sqrt{\frac{(s-b)(s-c)}{s(s-a)}} (dividing sinA/2 by cosA/2)

6) Formulae for Area:

\Delta = \frac{1}{2}bc\; sinA=\frac{1}{2}ca\; sinB=\frac{1}{2}ab\; sinC

\Delta = \frac{abc}{4R}

\Delta = \sqrt{s(s-a)(s-b)(s-c)}

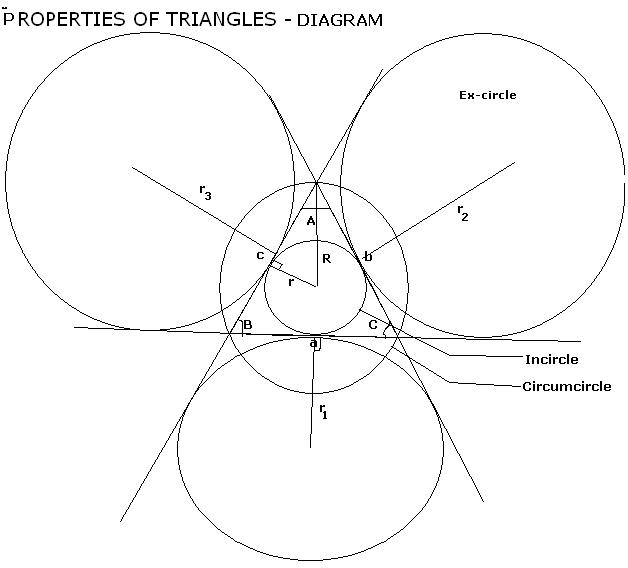
7) Formulae for R (circumradius):

R= \frac{abc}{4\Delta }

R= \frac{a}{2\; sinA}=\frac{b}{2\; sinB}=\frac{c}{2\; sinC }\; \; \; \left(from\; Sine\; Rule \right)

8) Formulae for r (inradius):

r= \frac{\Delta }{s}=(s-a)tan\frac{A}{2}=(s-b)tan\frac{B}{2}=(s-c)tan\frac{C}{2}

r= 4R\; sin\frac{A}{2}\; sin\frac{B}{2}\; sin\frac{C}{2}

9) Formulae For r₁, r₂ and r₃( ex-radii):

r_1=s\; tan\frac{A}{2}

r_2=s\; tan\frac{B}{2}

r_3=s\; tan\frac{C}{2}

r_1= 4R\; sin(\frac{A}{2})\; cos(\frac{B}{2})\; cos(\frac{C}{2})

r_2= 4R\; cos(\frac{A}{2})\; sin(\frac{B}{2})\; cos(\frac{C}{2})

r_3= 4R\; cos(\frac{A}{2})\; cos(\frac{B}{2})\; sin(\frac{C}{2})

ALL THE BEST [4]

FANTASTIC JOB [1]