1its not cos2x its cos2x
1.Prove that sin(3x) = 4sinx.sin2x.sin4x
2.Solve : cosx(1+sin x/4 - 2cosx) + sinx (cosx/4 - 2sinx) = 0
3.solve : cos 3x + cos 2x = sin 3x/2 + sin x/2 , x=(0,pi)
4.solve for x and y : cos2x + cosx.cosy + cos2y = 0
-
UP 0 DOWN 0 0 6
6 Answers
62cos2x + cosx.cosy + cos2y = 0
The best you can do here is to write a quadratic in cos x and then find the value of cos x in terms of cos y and then keep it like that...
I even tried matlab on that one....
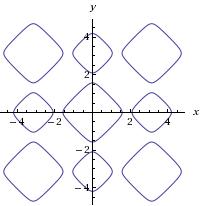
This is how it looks!
62cos2x + cosx.cosy + cos2y = 0
Then it is even worse..
We can say that this is same as (cos x/cosy) = t
then t2+t+1 = 0
has no solution..
Hence the given equation is never true!
62sin(3x) = 4sinx.sin2x.sin4x
use sin 3x = 4 sin x sin (60-x) sin (60+x)
4 sin x is zero is one option
or otherwise sin(60-x)sin(60+x)=sin 2x sin 4x....
now try?