if i remember correctly this is a question from the book mathematical olympiad challenges by titu andrescue(cant ever spelll his name properly)
ABC is an equilateral triangle.
P is any point in it satisfying PA=3, PB=4 & PC=5 units.
Find area of the triangle.
-
UP 0 DOWN 0 2 15

15 Answers
first method:
not giving it much of a thought as of now:
but using cosine rule u can find the cos PAPB and cos APC and cos BPC in terms of a . now use that the sum of these three angles is 360 degrees and use
cos(x+y+z)=(Σ cosx -π cosx)/(1-Σ cosxcosy)
so u get a. now area can be found
second method:
this came to to my brain while i was driving today.....
let the distances of P a interior point in an equilaeral triangle be a,b,c
let the side of the triangle be `d`
then the following relation holds good:
3(a4+b4+c4+d4)=(a2+b2+c2+d2)2
hmm.. how can someone get this relation while driving!
I cant see an obvious reason... Is there some help?
Fiitjee has given a remarkably nice soln for this....I dunno whether that's copied or not, but I think that technique will help us all in simplifying the complicate problems .........Can someone do this by a non-routine way-kinda-stuff......?
I shall post Fiitjee's soln if no-one turns up with something else.
Does it have to do with using Heron's formula? Looks unlikely
Can u give a clue what approach they used?
Has it to do with (A+B+C) = 360
cos(A+B) = cos(C)
I can also see cosine formula.. for each angle APB, APC and BPC (since the 3rd side is equal)
Other than that there is pythagoras theorem..
But then all these dont seem to help me solve the puzzle :(
They have rotated triangle ABC through vertex A by an angle \frac{\pi}{3} in clockwise direction.
wrt #7 , these were some proofs that i had solved while preparing for RMO in 11th class.
P being a point inside equilateral triangle, we have got a quite a good number of interesting and challenging results to be proven..
pmpeiu triangle is one more such thing related to same P,A,B,C
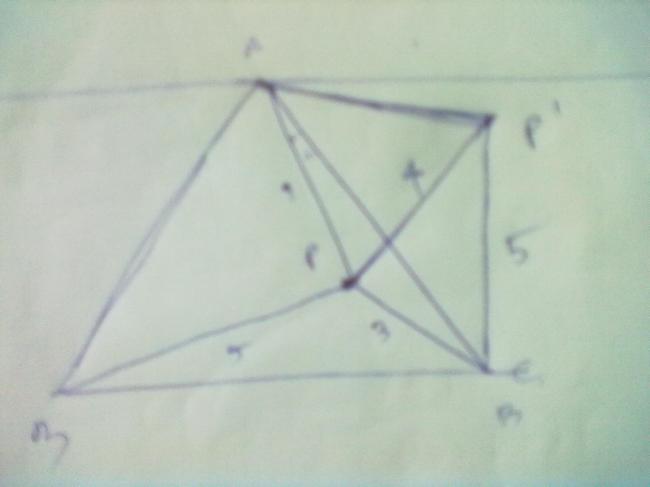
I'd rotate it anticlockwise.Consider a rotation R_A with center at A,such that R_A:B\overset{+\pi/3}{\rightarrow}B_1 = C\; \; \;, \; \; R_A:P\overset{+\pi/3}{\rightarrow}P_1
Since Rotation preserves angle and length,PB= P_1B_1= P_1C = 5 and \triangle APP_1 is equilateral. so PP_1= AP= 4.In \triangle PP_1C, PP_1= 4,PC= 3,P_1C= 5, so \angle P_1PC = \frac \pi 2. So \angle APC=\angle APP_1 + \angle P_1PC= \frac {5\pi} 6. From Cosine rule on \triangle APC, AC= \sqrt{AP^2 + PC^2 - 2\cdot AP\cdot PC \cdot \cos(\angle APC)}= \sqrt{25+ 12 \sqrt{3}}. Area is east to find out from here...
- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -- - - - - - - - -
the motivation is to form a triangle with the given sides...Thanks devil for the hint :P
I think u wont get it from the method told by b555(after eliminating variables, it gives scary equations)...or from any such trigo approach...thats why its nice...