303. 
Rx (Net horizontal component) = k + k/√2 - k/√2
Ry (Net vertical component) = - (k + k/√2 + k/√2)
Therefore,
Resultant(R) = k i - (k +√2k) j
|R| = √k2 + k2(3 + 2√2)
= k√4+2√2
Option 3.
I already knw da answers to the followin questions. I am interested 2 knw da solution.Pls solve dem guys.
I) |(a x b).c| = |a||b||c| ,if
(1)a.b=b.c=0 (2)b.c=c.a=0 (3)c.a=a.b=0 (4)a.b=b.c=c.a=0
II) If b and c are two non-collinear vectors such that a || (bxc), then (axb).(axc) is equal to
(1)a2(b.c) (2)b2(a.c) (3)c2(a.b) (4)None of these
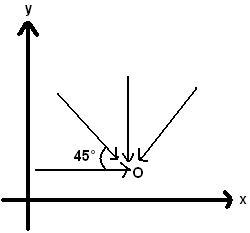
III) Four coplanar forces are applied at a point O. Each of them is equal to k and the angle between two consecutive forces equals 45° .Then the resultant has a magnitude equal to:
(1)k√2+2√2 (2)k√3+2√2 (3)k√4+2√2 (4)None of these
IV) Given the vertices A(2,3,1), B(4,1,-2), C(6,3,7) & D(-5,-4,8) of a tetrahedron. The length of the altitude drawn from the vertex D is:
(1)7 (2)9 (3)11 (4)None of these
*in da last ques if the solution is too long and inconvinient to b posted here, then jus tell me what formula and what method/procedure to apply to do the sum. Thanx.
-
UP 0 DOWN 0 0 5
5 Answers
301) \left|(\vec{a }\times \vec{b})\cdot \vec{c }\right|=\left|(\left|\vec{a} \right|\left| \vec{b}\right| sin\theta \hat{n} )\cdot \left| \vec{c}\right| \hat{k}\right|
= \left|\left| \vec{a}\right| \left| \vec{b}\right|\left| \vec{c}\right|sin\theta \left| \hat{n}\right|\left| \hat{k}\right|cos\phi \right|
= \left| \vec{a}\right| \left| \vec{b}\right|\left| \vec{c}\right|\left| \hat{n}\right|\left| \hat{k}\right|sin\theta cos\phi \: ... (i)
From (i),
\left| \vec{a}\right| \left| \vec{b}\right|\left| \vec{c}\right|\left| \hat{n}\right|\left| \hat{k}\right|sin\theta cos\phi = \left| \vec{a}\right| \left| \vec{b}\right|\left| \vec{c}\right|
\Rightarrow sin\theta cos\phi = 1
Clearly,
\theta = \pi /2 \:\: and\:\: \phi =0
Hence, option 4.
30
1for the fourth one its simple
take A(x1,y1,z1)
B(x2,y2,z2)
C(x3,y3,z3)
equation of plane passing through A,B,C is given by the following determinamt
(actually there will be three equations which can be solved be determinants)
let the equation of the plane be
ax+by+cz=d..........................................................eqn4
egn is satisified by A,b coz A passes through plane
ax1+by1+cz1=d.....................................................eqn5
from A and B,we get a eqn of a plane passing through A
a(x-x1)+b(y-y1)+c(z-z1)=0.........................................eqn1
This plane contains points B and C also, so:-
a(x2-x1)+b(y2-y1)+c(z2-z1)=0.........................................eqn2
a(x3-x1)+b(y3-y1)+c(z3-z1)=0.........................................eqn3
using euations 1,2,3
Eliminale a,b,c by determinant
| (x-x1) (y-y1) (z-z1)|
|(x2-x1) (y2-y1) (z2-z1)| =0...............................................eqn 6
|(x3-x1) (y3-y1) (z3-z1)|
,(i can't write determinant symbol,its a3rd order determinant)
the eqn obtained from six is in the form
Px+Qy+Rz-S=0
let D be (x4,y4,z4)
len=Px4+Qy4+Rz4-S√(P2+Q2+R2)
