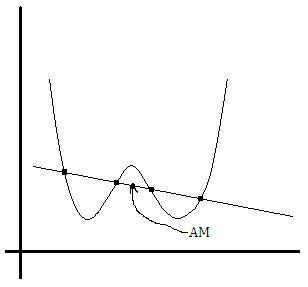
In any way ... karna is a better mathematician !!! lol
→if four points on the curve 2x4+7x3+3x-5 are colinear then find the A.M of the x coordinate of the four numbers?
1>-7/8
2>7/8
3>3/4
4>-3/4
-
UP 0 DOWN 0 0 21

21 Answers
How could karna plug the line eqn. into the curve eqn. without actually knowing whether the variable line cuts the curve at all ? Because if you differentiate his eqn. , you get
d/dx of curve = λ , which according to you guys is suggesting that the points are lying on a tangent , on which they are actually not lying.
Pritish Bhai i didn't say Karna is wrong... Soumya is wrong not karna. Karna is absolutely right.
where is karna's method wrong? Four points ON the curve, collinear, jinka AM nikaalna hai so we primarily need the sum of the roots of the equation with the straight line equation formed by those 4 points. The curve is real, and if points are on the curve, they have to be real too..?
Subho...what does cutting the curve with the x-axis have to do with collinearity of four points on the curve? We needn't bother with the y coordinates of the newly formed equation....
Arrey Swaraj Bhai ... it's not tangency but collinearity that matters.......All points are passing through the same line.
And as for your confusion , u r right. Soumya's proof tis wrong. Slope of curve is not the slope of the line thru the 4 pts. Slopeof thecurve or dy/dx is the tangent to the curve ,,,,, BOT A LINE INTERSECTING IT... so swaraj is right.
but i think it is not correct that slope of he curve at these four points should be equal.bcoz the line is not the tangent at these points
Let's look into this in a different manner .
d / dx of this curve will give us the slope of the curve .
Now for those four points , slope of the curve would be same as the pts. are collinear , i.e , lie on the same line .
So we get d/dx ( curve) = h -----------------------( h is the slope)
Keep in mind that this eqn. holds only for those points.
Integrate both sides ,
we get original curve eqn = hx + c --------------------- ( where c is the constant of integration )
Now plug this into your solution , and shubho , this should clear your doubt .
bt hw do u kno all the roots are real????
may be the points are collinear on some other st line....]
maybe the curve do not cut x-axis at all
the curve of fourth power of x is something having a w like shape...a straight line will pass through the 4 faces of the W.....
i just screwed it up...lol
we just need to equate the two equations.....but that is a gadha ghora method....is there nothing simpler........nishant bhaiya!!!!!!!!!!`
sorry guys i misread the question we have to find the avg of x-coordinates
hello subhomo can u say me wheather the curve is symetric about the middle edge or not
no the previous solution is wrong....but i have most probably found out something better..
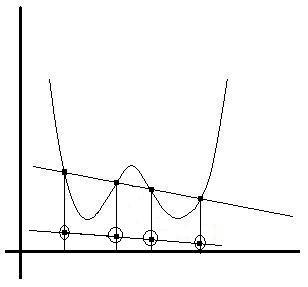
we have to find the sum of the y-coordinates of the encircled points.....these points are located at a distance 1/4 of y-coordinates of corresponding above points....
AM=(y1+y2+y3+y4)/4
=y'1+y'2+y'3+y'4
now for lower lying line, y'=y/4(where y is y-coordinate of corresponding above lying st. line)
so, y'=(λ/4)x+(c/4)
let y=λx+c
and y=2x4+3x3-x+5
i need hints.....swaraj da....wat 2 do nxt??
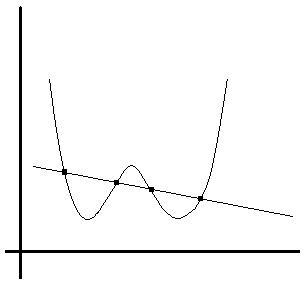
now the problem is that we have to find the AM of the 4 points..