1okies sir ! [1][3]
3C4 is 0 only .
reminds me of qwerty's signature
A polynomial f(x) of n-th degree satis
es f(k) = 2k for k = 0, 1, 2,.... n
Find f(n + 1)
(I was wondering if I should put it in the olympiad section.. but then with the last few discussions on polynomials that we have.. I thought this could rather stay in the normal section...
Btw I did not attempt this one myself.. bcos I was tempted to see the solution.. (Which is awesome :D) *Edited..
-
UP 0 DOWN 0 0 26
26 Answers
1this is the part missing in bhargav bhaiya's solution
here we should assume a polynomial
g(k)= f(k)-2k = 0
we observe that it is a polynomial with degree n . but as given it is satisfied by (n+1) values 0,1,2,3...n.
thus it is an identity .
=> f(k)=2k for all values of k .
thus now proceding as bhargav bhaiya.
62haha.. yeah 5 out of 4 people will not understand the joke nor why 5C4=0 :P
3mmm sir actually i thot of the binomial theorem written by u,but din postd some wat is missing or something i cant understand,donno how to express my dbts,frankly i am not fully satisfid with the soln,dunno y.:P
62yes karna it is ...
but what is the value of 3C4 .. it is zero..
so it does not change anything [1]
@sankara.. no it just an after thought after what bhargav has done..
nC0+nC1+...nCn = 2^n is very very obvious.
but if you want that to be a polynomial, what i would do is to somehow reconstruct it as a polynomial.
so the polynomial is just looked in 2 ways.. one as karna rightly said (generalized binomial thoerem) or equivalently what i have written.
3mmm i am not asking dat bro,i was asking him wat made him to get a function like dat.
1@msp.the function is coming from binomial theorem for any index .
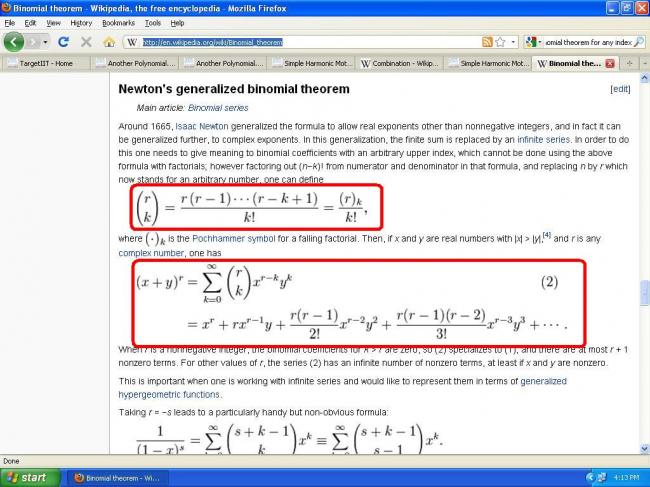
sorry i highlited the wrong equation b4 [3]
3sir how to get the function,is dat by observation,or nething to think more.
1okies sir......
but b555 's function is wrong as
in his function
f(3)=3C0 +3C1 +3C2 +3C3 +3C4(?)+..
but ur function takes care of the other terms by making them 0
isn it binomial expansion for any index ?
62With what bhargav has done, if we could make a very small adjustment to define the function for all x and not just for integers, we can either use the alternative definition of nCr for non integers or use the following polynomial:
f(x)=1+x+\frac{x(x-1)}{2}+\frac{x(x-1)(x-2)}{2.3}+...+\frac{x(x-1)(x-2)...(x-n+1)}{1.2.3...n}
This will look like what bhargav has written if x is an integer
and with this function in mind (which is a polynomial in n degree) we proceed like how bhargav has in his post
[1]
62yes karna you are right..
and that is why i posted the reservations in the next few posts...
I will give the complete proof.
[1]
1sir but b555 function isnt defined for all real values..
whereas a polynomial must be defined for al real values
62but 2^k is not a polynomial at all..
That is not what bhargav meant ...
62Bhargav are u sure it is out of syllabus?! :D
I think you have not understood the spirit of your own solution :P ;)
3well i have dbt,even i thot of expanding by binomial.But i left it becos f(x) is defined for all real values of x,also the given f(x) doesnt defined for negative x na.
39now the explanation i have will for sure go out jee sylabus
so i would be glad to see someone post a explanation that everyne can understand
62A few things that you have not explained at all..
what was athe need of the polynomial having n roots
and why should the polynomial take the same value at n+1 ??? ?
39here, we see that
f(x)=x_{C_{0}}+x_{C_{1}}+x_{C_{2}}+.......................+x_{C_{n}}
so we have
f(n+1)=(n+1)_{C_{0}}+(n+1)_{C_{1}}+(n+1)_{C_{2}}+.......................+(n+1)_{C_{n}}
=2^{(n+1)}-1
[ since here we have the sum of coefficients of (1+x)^{(n+1)} which is equal to 2^{(n+1)}]
3hey dude if u know the soln,y dont u give me a hint for me,ne hint that is within the syllabus of jee.
39well nishant sir , shall i finish it off or u want to wait for some more days?
between did u get the hint in what i said in #7?
i have no doubt that bhatt sir would have obviously understood what i meant.
62Yes it is not...
and you have to think of something really tricky to get over this one!
