1@eureka . where are these problems on binomial from ? (if you dont mind.)
If a0,a1,a2.... be the coefficients in the expasion of (1+x+x2)n in ascending power of x
then prove that
1) (r+1)a_{r+1}=(n-r)a_r+(2n-r+1)a_{r-1};0<r<2n
2)(a_0+a_3+a_6+...)=(a_1+a_4+a_7+...)=(a_2+a_5+a_8+...)=3^{n-1}
i tried this one by putting x=1,ω,ω2..but couldnt complete it..plz help
-
UP 0 DOWN 0 1 4
4 Answers
1
62Let the expression be equal to
\\f(x)=a_0+a_1x+a_2x^2+...+a_rx^r+...+a_{2n}x^{2n} \\f(1)=3^n=a_0+a_1+a_2+...+a_r+...+a_{2n} \\f(w)=0=a_0+a_1w+a_2w^2+...+a_rw^r+...+a_{2n}w^{2n} \\f(w^2)=0=a_0+a_1w^2+a_2(w^2)^2+...+a_r(w^2)^r+...+a_{2n}(w^2)^{2n}
Adding the three,
3^n=3a_0+3a_3+...+3a_{3r}+...
Hence the proof of one part...
Try the other two..... :)
11For part 1) (1+x+x2) n =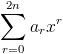 
............(i)
Differentiate w.r.t x , we get
n (1+2x) (1+x+x2) n-1 =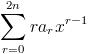 
Multiplying both sides by (1+x+x2) , we get
n (1+2x) (1+x+x2) n = (1+x+X2) image]35086847.jpg[/image]
n(1+2x) 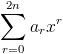= (1+x+X2)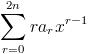
.....................[from (i)]
Equating the coeff of x r , we get
n a r + 2n a r-1 = (r+1) a r+1 + r a r + (r-1) a r-1
(r+1) a r+1 = (n-r) a r + (2n-r+1) a r-1
Thus Proved.
