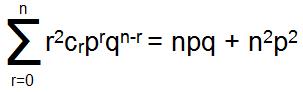1708$Here $r^2.\binom{n}{r}=r^2.\frac{n}{r}.\binom{n-1}{r-1}=n(\underbrace{r-1}+1).\binom{n-1}{r-1}$\\\\ $=n.(r-1)\binom{n-1}{r-1}+n.\binom{n-1}{r-1}$\\\\ $=n.(r-1).\frac{n-1}{r-1}.\binom{n-2}{r-2}+n.\binom{n-1}{r-1}=n.(n-1).\binom{n-2}{r-2}+n.\binom{n-1}{r-1}$\\\\ So $\boxed{r^2.\binom{n}{r}=n.(n-1).\binom{n-2}{r-2}+n.\binom{n-1}{r-1}}$\\\\ Now here We have To calculate\\\\ $\sum_{r=0}^{n}.r^2.\binom{n}{r}.p^r.q^{n-r}=n.(n-1).p^2\sum_{r=2}^{n}.\binom{n-2}{r-2}.p^{r-2}.q^{(n-2)-(r-2)}+n.p.\sum_{r=1}^{n}.\binom{n-1}{r-1}.p^{r-1}.q^{(n-1)-(r-1)}$\\\\ $=n.(n-1).p^2.(p+q)^{n-2}+n.p.(p+q)^{n-1}$\\\\ (Using The formula $\sum_{r=0}^{n}.\binom{n}{r}x^r.y^{n-r}=(x+y)^n$)\\\\ $=n.(n-1).p^2+n.p=np.(np-p+1)=np.(np+\underbrace{1-p})=np.(np+q)$\ $=n^2p^2+npq$. (bcz $p+q=1$ and $q=1-p)$\\\\ So $\boxed{\boxed{\sum_{r=0}^{n}r^2.\binom{n}{r}.p^r.q^{n-r}=n^2p^2+npq}}$
