Ai's are reals, so are ais, while n is natural!
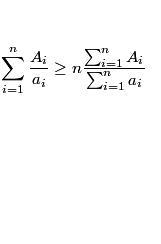
I suddenly encountered this inequality (While attempting another one [78] ), which seemingly seems true....(I mean I checked with a few values....) but i've not been able to prove it, as it is I do not even know whether this holds for all reals or not....so it's time for some expert's opinion!
-
UP 0 DOWN 0 0 16

16 Answers
i think its some form of titu lemma inequality theorem....
check this out
http://get-set-go-jee.lefora.com/2009/08/31/titus-lemma/page1/#post14681747
1 thing that I forgot to mention was Ai<ai, and all are positive reals....
what you have written is same as
\large \Sigma{(x_i)}\times\Sigma{(y_i)}\geq n\times \Sigma {(x_iy_i)}
where xi<1
CAN U PLS ELABORATE A BIT MORE NISHANT SIR..... I dunno wat's wrong with my head, may be it's mugged up with rubbish ideas....
i mean my inequality meant kinda this....
ab+cd+.......(n terms) ≥ na+c+....b+d+....
yup.. i can see that.. and i dont see why Ai< ai will make any difference.. in any case you can divide the numerator on both sides by a large number to get somethign small....
what i have written is your same expression cross multiplied..
xi=Ai/ai
and yi=ai
Can some divine grace turn up and elegantly confirm me whether this holds for all positive reals and naturals?
Thanx Nishant sir 4 the help....
take x1=1/200, x2=1/2
y1=1, y2=100
now check... (I gave the logic why we dont need x1<1 ;)
This looks like Chebyshev at work. So the positive sequences {ai} and {Ai} have to be oppositely sorted in order that the sequences {ai} and {Ai/ai} are oppositely sorted
yes that was my first impression too.. but then soumik has not mentioned this condition !!
And that is why i asked him to confirm from you if there is something like a rearrangement inequality working!
Well, let me sort out the confusion.....
{Ai} and {ai} are sequences of positive reals.....such that
Aiai<1 for all i......
now i hope it's clear.
nishant sir,
xi=Aiai=1200
x2=12
Adding x1 and x2we get 101200
Which should be > 2.2202
This is very much true!
no x1=1/200, x2=1/2
y1=1, y2=100
(X1+x2)=101/200
y1+y2=101
x1y1+x2y2=1/200+100/2 = 10001/200
(x1+x2)(y1+y2) = 101/200 * 101 = 10201/200
n*(x1y1+x2y2) = 2*10001/200 = 20002/200
THus, (x1+x2)(y1+y2) = 10201/200 while, n*(x1y1+x2y2) = 20002/200
Hence your inequality does not hold :P
If I have still made a mistake.. then check this link for chebychev's inequality on wikipedia.. and see the condition.. you will realize that you have not given us all the information about Ai and ai
Link Here:
http://en.wikipedia.org/wiki/Chebyshev%27s_sum_inequality